Bezpečné sdílení tajemství s využitím soustav lineárních rovnic
Jak bezpečně rozdělit utajenou informaci skupině lidí tak, aby ji byli schopni zrekonstruovat jen tehdy, sejde-li se jich dostatečný počet? Blakleyho schéma umožňuje problém řešit s pomocí metod známých z lineární algebry.
Proč sdílet tajemství
V dobrodružných filmech se mnohdy setkáváme se situacemi, kdy hrdinové musí spolupracovat, protože každý z nich je majitelem části informace nebo klíče vedoucího ke splnění jejich cíle. Může jít o mapu pokladu rozdělenou na několik částí či hesla k odpálení balistických raket, která mají v úschově armádní generálové. Takové situace ale nemusí být jen fiktivní. Můžeme si představit, že vedení firmy vyžaduje vytvoření systému, který umožní, že nákup či prodej akcií bude moci digitálním podpisem schválit generální ředitel nebo pět členů představenstva. Ve všech těchto případech máme co do činění s potřebou rozdělit utajenou informaci skupině jednotlivců či sdružení tak, aby bylo možné ji zrekonstruovat pouze, když se sejde dostatečný počet účastníků.
Specifikace požadavků
Je dost komplikované rozstřihnout papírovou mapu na dvě části tak, aby žádná část neumožnila svému majiteli poklad najít. S větším počtem podílníků je pak prakticky nemožné mapu rozdělit, neboť všichni zúčastnění jistě budou trvat na tom, že bez jejich dílu nesmí být ostatní schopni poklad vyzvednout. Zároveň je jasné, že dojde-li ke ztrátě nebo zničení některého dílu, bude nalezení pokladu nemožné. Jak uvidíme dále, mnohem snáze než mapu jsme schopni rozdělit např. GPS souřadnice udávající polohu pokladu.
Obecně je mnohem praktičtější, když sdílené tajemství představuje nějaká informace. V následujícím textu budeme tuto informaci vždy reprezentovat celým číslem $N\in \mathbb{Z}$. Je-li informací textový řetězec, lze mu numerickou hodnotu přiřadit např. pomocí ASCII kódu. Číslo $N$ ale může představovat i soukromý klíč šifrovacího systému RSA.
Standardní kryptografické postupy jsou vhodné k tomu, abychom citlivá data udržovali v bezpečí před prozrazením. Uchováváme-li ale data ve více kopiích, abychom předešli jejich ztrátě, má potenciální útočník více možností, jak se k utajené informaci dostat. Systém sdílení tajemství by proto měl poskytovat nejen vysoký stupeň zabezpečení, ale také vysokou spolehlivost, tzn. měl by umožnit zrekonstruovat utajenou informaci i v případě, že dojde ke ztrátě dat u některého z podílníků.
Pojďme nyní formalizovat naše požadavky. Je zadáno číslo $N\in \mathbb{Z}$ představující utajenou informaci.
$n$ podílníkům máme distribuovat informaci o $N$ tak, aby mohli jednoznačně určit $N$ sejde-li se alespoň $k$ z nich.
Sejde-li se nejvýše $k-1$ podílníků, nesmí o $N$ zjistit více než někdo, kdo žádný podíl na sdíleném tajemství nemá.
Jistě rozumíme případu kdy $n=k$. Pro situace, kdy představenstvo firmy má devět členů a chceme, aby každých pět z nich mohlo schválit burzovní operaci, je ovšem rozumné požadovat, aby systém zvládl i případ $n>k$. Pak lze totiž operaci autorizovat i když jsou čtyři členové nedostupní nebo o svá data přišli. Odolnost systému v případě ztráty části informace je tedy zaručena. K provedení operace je při tomto nastavení nutný souhlas většiny představenstva. Vyžadujeme-li navíc, aby mohl generální ředitel operaci schválit sám bez asistence představenstva, musí obdržet dalších pět podílů na sdíleném tajemství. Parametry schématu tedy budou $k=5$, $n=9+5=14$.
Naivní přístup
Jak schéma sdílení tajemství navrhnout? Při konstrukci systému můžeme zkusit rozdělit mezi podílníky přímo cifry $N$. Takový systém zjevně není bezpečný. Očekáváme-li, že $N$ má $6$ cifer a každý z podílníků zná dvě z nich, nemusí pro získání $N$ hrubou silou vyzkoušet $10^6$ možností, ale jen $10^4$. Pokud se dva podílníci spojí proti třetímu, stačí jim už vyzkoušet jen $10^2$ možností.
Jiný často zmiňovaný systém využívá operace XOR (eXclusive OR) značené $\oplus$. Reprezentujeme-li $N$ ve dvojkové soustavě pomocí $b$ bitů a náhodně vygenerujeme $n-1$ čísel $N_i,\ i\in \{1,\ldots, n-1\}$, kde každé má délku $b$ bitů, můžeme po jednotlivých bitech aplikovat XOR, spočíst \[ N_n=N\oplus N_1\oplus \ldots \oplus N_{n-1} \] a účastníkům distribuovat jednotlivá $N_i$. Sdílené $N$ lze pak znovu získat jako \[ N=N_1\oplus \ldots \oplus N_n, \] neboť platí, že $(a\oplus b)\oplus b = a\oplus (b\oplus b)=a$. Takový systém je bezpečný, protože kdykoliv se sejde méně než $n$ podílníků, mohou dát dohromady pouze náhodné $b$-bitové číslo. V tomto systému je ale k zjištění $N$ potřeba mít k dispozici všech $n$ podílů. V následující části si přiblížíme schéma, které je bezpečné a přitom nevyžaduje přítomnost všech $n$ podílů.
Blakleyho schéma - sdílení lineárních rovnic
V roce 1979 představil G. R. Blakley v článku [1] schéma sdílení tajemství využívající soustav lineárních rovnic. Pro názornost schéma nejprve představíme v poněkud zjednodušené podobě. Zvolíme náhodně bod $P=(y_1, \ldots , y_k)$ v $\mathbb{R}^k$ tak, aby pro všechna $j\in\{1,\ldots,k\}$ platilo $y_j \in \mathbb{Z}$. První složka $y_1$ bodu $P$ bude představovat sdílené tajemství $N$.
Každému z $n$ podílníků poté svěříme jednu lineární rovnici pro $k$ neznámých $x_j$, kterou bod $P$ splňuje. $i$-tý podílník obdrží jednu rovnici \[ a_{i1} x_1 + \ldots + a_{ik} x_k = b_i, \qquad a_{ij}, b_i \in \mathbb{R}, \] kde $i\in\{1,\ldots,n\}$, $j\in\{1,\ldots,k\}$. Rovnice určuje nadrovinu v $\mathbb{R}^k$ procházející bodem $P$. Máme-li stejně jako na obrázku 1 k dispozici $k$ nadrovin jejichž společným průnikem je jediný bod $P$, má i soustava rovnic \begin{equation}\label{soustava} \begin{matrix} a_{11}x_1 & + & \cdots & + & a_{1k}x_k & = & b_1, \\ \vdots & & \ddots & & \vdots & & \vdots \\ a_{k1}x_1 & + & \cdots & + & a_{kk}x_k & = & b_k \end{matrix} \end{equation} jediné řešení, kterým je bod $P$. Sejde-li se $k$ podílníků, získají složky bodu $P$ a tedy i sdílené tajemství $N=y_1$ jako řešení soustavy rovnic \eqref{soustava}.
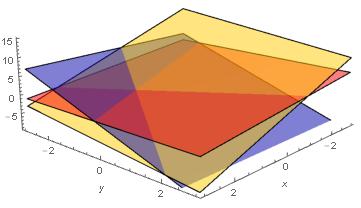
Obrázek 1: Průnikem tří nadrovin v $\mathbb{R}^3$ zadaných rovnicemi \eqref{pr:soustava_rovnic} je jediný bod $P=(1,-1,1)$.
Pro existenci jednoznačně daného řešení je přitom zásadní, aby tyto rovnice byly nezávislé. Jinými slovy, matice $\mathbb{A}$ koeficientů levé strany soustavy musí mít nenulový determinant. Tato podmínka odpovídá požadavku, aby normálové vektory $(a_{i1}, \ldots, a_{ik})$ určující nadroviny byly lineárně nezávislé.
Snadno nahlédneme, že sejde-li se $k-1$ podílníků, dají dohromady soustavu, jejímž řešením je přímka. Sdílené tajemství $N$ obsažené v první složce $P$ tedy nelze zjistit, pokud nezvolíme rovnice tak nešikovně, že tato přímka má konstantní první souřadnici.
Nadrovin procházejících bodem $P$ lze ale zkonstruovat nekonečně mnoho a schéma je proto vhodné i v situaci, kdy má být počet podílníků $n$ větší než minimální počet podílů $k$ nutných k určení $N$. Rovnici nadroviny procházející bodem $P$ lze získat tak, že náhodně vygenerujeme koeficienty $a_{ij}$ levé strany rovnice a dosazením $y_j$ za neznámé dopočteme pravou stranu $b_i$. Při generování rovnic ovšem musíme mít na paměti to, že pro každou $k$-tici rovnic musí existovat právě jedno řešení, tedy že determinant matice koeficientů levé strany příslušné soustavy musí být nenulový. Přidání další rovnice přitom ostatní nijak neovlivní. V případě potřeby lze proto navýšit počet podílníků $n$, aniž bychom museli stávajícím podílníkům distribuovat nová data.
Příklad 1
Schéma můžeme demonstrovat na jednoduchém příkladu. Mějme čtyři podílníky, kteří chtějí sdílet tajné $N$ tak, aby ho mohli určit jen tehdy, sejdou-li se alespoň tři z nich. Je-li $N=1$, můžeme zvolit bod $P$ jako $P=(1,-1,1)$ a postupně prvním třem podílníkům distribuovat lineárně nezávislé rovnice \begin{equation}\label{pr:soustava_rovnic} 3x+y+z=2,\qquad 3y + z= -5,\qquad x+z=2. \end{equation} V $\mathbb{R}^3$ pochopitelně nelze vytvořit čtyři lineárně nezávislé rovnice. Předáme-li čtvrtému podílníkovi rovnici \begin{equation}\label{pr:soustava_rovnic2} x+y+z=1, \end{equation} bude libovolná trojice rovnic nezávislá a bude tedy jednoznačně určovat bod $P$. Na obrázku 2 vidíme, že průnikem čtyř nadrovin zadaných rovnicemi \eqref{pr:soustava_rovnic} a \eqref{pr:soustava_rovnic2} je právě bod $P$. K jeho určení však stačí pouze tři nadroviny. Na obrázcích 1 a 2 je rovina určená první rovnicí z \eqref{pr:soustava_rovnic} vyznačena žlutě, rovina určená druhou rovnicí je značena modře a třetí červeně. Rovina určená rovnicí \eqref{pr:soustava_rovnic2} je v obrázku 2 značena zeleně.
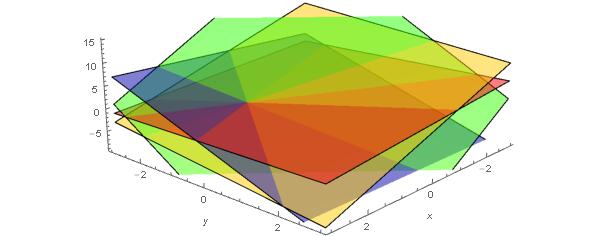
Obrázek 2: Průnik čtyř nadrovin v $\mathbb{R}^3$ zadaných rovnicemi \eqref{pr:soustava_rovnic} a \eqref{pr:soustava_rovnic2}.
Proč by mělo být sdílené tajemství $N$ obsaženo pouze v jedné souřadnici bodu $P$? Pokud by informace byla obsažena ve všech složkách $P$, mohl by se jistě zmenšit objem dat, která je nutno uchovávat. Stejně jako při naivním přístupu v části 3 by ale schéma nebylo bezpečné, neboť při znalosti jedné rovnice by podílník již měl částečnou informaci o $N$. Věděl by totiž, že $P$ leží v příslušné nadrovině.
Blakleyho schéma jsme pro názornost popisovali pomocí soustav lineárních rovnic nad $\mathbb{R}$. Pokud ovšem útočník očekává celočíselná řešení a má k dispozici jednu nebo více rovnic, může se pokusit danou soustavu řešit v celočíselném oboru jako soustavu lineárních diofantických rovnic, což může útok ulehčit. Mohli bychom slevit z požadavku celočíselnosti souřadnic $y_j$ a za sdílené tajemství $N$ prohlásit třeba několik prvních platných cifer reálného čísla $y_1$. Tím bychom se ale nevyhnuli numerickým chybám vznikajícím při počítání s reálnými čísly reprezentovanými na počítači ve formátu float. Je proto mnohem elegantnější zvolit dostatečně velké prvočíslo $p$ takové že $N<p$ a soustavy rovnic uvažovat nad konečným tělesem $\mathbb{Z}_p$, kdy standardní operace sčítání a násobení uvažujeme modulo $p$. Zvolíme tedy náhodně bod $P$ jako \[ P=(y_1, \ldots, y_k), \qquad y_1=N, \qquad y_j \in \mathbb{Z}_p \] a podílníkům distribuujeme rovnice \[ a_{i1} x_1 + \ldots + a_{ik} x_k = b_i, \qquad a_{ij}, b_i \in \mathbb{Z}_p, \]
generované tak, aby každá $k$-tice rovnic byla nezávislá. To lze opět ověřit výpočtem příslušného determinantu, který musí být nenulový modulo $p$. Pravděpodobnost nalezení takových rovnic pomocí náhodné volby koeficientů $a_{ij}, b_i \in \mathbb{Z}_p$ je detailně diskutována v článku [1].
Příklad 2
Pro čtyři podílníky z předchozího příkladu můžeme zvolit například $p=17$ a každému svěřit jednu z rovnic \begin{align*} x+2y+3z & = 3,\\ 3x+5y + 4z & = 4,\\ 2x+4y+7z & = 3,\\ 2x+5y+8z & = 3. \end{align*} Můžeme se přesvědčit, že každá trojice těchto rovnic je lineárně nezávislá, že každé dvě rovnice mají za řešení přímku s nekonstantní první souřadnicí a že společným řešením v $\mathbb{Z}_{17}^3$ je bod $P=(6,3,14)$. Vybereme-li kupříkladu první dvě rovnice, je jejich řešením v $\mathbb{Z}_{17}$ množina o $p=17$ prvcích zadaná jako \[ x = 10 + 7 t,\quad y = 5 + 12 t,\quad z = 0 + t, \quad t\in\{0, \ldots , 16\}. \] Zde $x$ nabývá všech možných hodnot v $\mathbb{Z}_p$. Znalost dvou rovnic proto nijak neumožní určit utajené $N$.
Při práci s konečnými tělesy můžeme také dobře prozkoumat odolnost systému vůči útoku hrubou silou. Jelikož je sdílené tajemství $N\in\mathbb{Z}_p$ obsaženo v první souřadnici bodu $P$, může nabývat $p$ hodnot. Sejde-li se $k-1$ podílníků, řešením jejich soustavy rovnic je přímka v $\mathbb{Z}_p^k$, která ovšem také obsahuje $p$ bodů. Ani $k-1$ podílníků tedy nemá o $N$ více informací než někdo, kdo žádný podíl na tajemství nemá.
Paměťové nároky Blakleyho schématu
V předchozím textu jsme se seznámili s Blakleyho schématem, které umožňuje $n$ podílníkům sdílet utajenou informaci $N$ tak, že je možno tuto informaci zjistit pouze sejde-li se alespoň $k$ podílníků. Schéma využívalo soustav lineárních rovnic nad $\mathbb{R}$ či $\mathbb{Z}_p$. Pracujeme-li v $\mathbb{Z}_p$, kde $N$ a $p$ jsou $b$-bitová čísla, musíme očekávat, že každý z koeficientů $a_{ij}$ a $b_i$ vystupujících v lineárních rovnicích bude opět $b$-bitové číslo. Pro uchování jedné rovnice je potřeba $(k+1)b$ bitů, což může znamenat velký objem dat. Systém navržený nezávisle A. Shamirem v článku [2] je v tomto ohledu mnohem efektivnější, přestože jsou obě schémata v základu ekvivalentní. Ačkoliv zmiňované systémy nejsou žádnou novinkou a Blakleyho schéma uvádíme spíše pro ilustraci problematiky, téma je velmi živé a v oblasti probíhá intenzivní výzkum.
- Blakley, G. R., Safeguarding cryptographic keys, American Federation of Information Processing Societies. National Computer Conference, 313-317 (1979)
- Shamir, A., How to share a secret, Communications of the ACM 22, 612-613 (1979).
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).

