Iracionální čísla
Štěpán Starosta, publikován 31. 10. 2017, editován 26. 10. 2018
Hodnoty, které můžeme naměřit jako délky úseček v našem světě jsou tzv. reálná čísla. Mezi těmito hodnotami lze objevit několik typově rozdílných čísel. V tomto textu se budeme věnovat především číslům iracionálním, tedy číslům, která nelze zapsat jako zlomek.
$\DeclareMathOperator{\fl}{fl} \newcommand\Fl[1]{\fl \left ( #1 \right)}$ $\newcommand\Q{\mathbb{Q}} \newcommand\Z{\mathbb{Z}}$
Připomeňme nejprve, co to vlastně jsou takzvaná racionální čísla. Čtenáře, který se s racionálními čísly přátelí, zveme ke smělému přeskočení této části a pokračování přímo v části zabývající se iracionálními čísly.
Racionální čísla
Celá čísla jsou abstraktním pojmem, který nám umožňuje popisovat jistou konkrétní podobnost mezi množinami nějakých objektů. Přesněji nám pomáhá popsat jejich počet, včetně počtu záporného. Záporná čísla lze též chápat jako vlastnost počtu objektů, ale z pohledu dluhu - vyjádříme jimi počet objektů, který nám chybí, abychom dosáhli neutrálního stavu, tedy nuly. Racionální čísla jsou rozšířením pojmu celých čísel o schopnost popsat skutečnost, že u nějakých objektů máme jen jejich část. Jak přesně tedy lze racionální čísla zavést?
Celá čísla nám budou sloužit jako výchozí hodnoty, které budeme dělit na části. Umíme s nimi násobit: v hledišti, které má $r$ řad a v každé řadě je lavice s $m$ místy, pohodlně pojme $r \cdot m$ diváků. S novými hodnotami reprezentujícími části budeme také chtít umět násobit. Násobení nám zároveň pomůže určit velikost části, na kterou celé číslo rozdělíme. Přesněji rozdělíme $m$ celků na $n$ stejných dílů. Poznamenejme, že počet dílů $n$, na který celek dělíme, dává dobrý smysl pouze pro $n$ přirozené, a takové jej tedy uvažujeme. Složením všech těchto dílů dostaneme hodnotu $m$. Toto si lze představit tak, že na lavici v jedné řadě s $m$ místy vyznačíme nová místa tak, aby vzniklo přesně $n$ stejných částí lavice.
Jeden tento díl má hodnotu označenou \[ \frac{m}{n}. \] Tento zápis se nazývá zlomek. O čísle $m$ se hovoří jako o čitateli, udává počet dílů. O čísle $n$ pak jako o jmenovateli, neboť nám díly pojmenovává. Zlomky si lze jednoduše představovat, na následujícím obrázku je dělení celků na celé části znázorněno na „koláčích“.

Obrázek č. 1: Ukázka zlomků jako části koláčů. Koláče jsou znázorněny kruhy a zlomky jsou tmavě zobrazené části.
Podstatná (a zatím jediná zmíněná) vlastnost zlomku $\frac{m}{n}$ je, že sečteme-li ho $n$-krát, dostaneme celé číslo $m$. Podobně jako u celých čísel tuto vlastnost podchytíme násobením a od zlomků budeme požadovat následující: \[ n \cdot \frac{m}{n} = m. \] Skládání stejných zlomků ilustruje následující obrázek.

Obrázek č. 2: Skládání stejných zlomků. Celky jsou zobrazeny jako koláče - kruhy. Zlomky jako tmavé části.
Abychom mohli o zlomku hovořit jako o nějaké hodnotě nebo číslu, musíme si vyjasnit ještě jeho další vlastnosti. Násobení číslem $n$ je velice nepostačující. Rádi bychom tyto nové hodnoty uměli násobit a sčítat, a také porovnávat. Prvním rozumným požadavkem je, že tyto vlastnosti budou kompatibilní s odpovídajícím vlastnostmi celých čísel.
Nejprve si ukážeme, jak zlomky násobit. <!-- Umění násobit celá čísla tedy rovnou implicitně rozšiřujeme o umění násobit i jejich poměry. --> <!-- Je to ovšem několik otázek. --> První otázkou je, co se stane, když $\frac{m}{n}$ vynásobíme číslem $k$, které se nerovná $n$? Výsledek si lze představit na skládání stejných dílů, nebo také vyjít z toho, že násobení je komutativní a mělo by být i pro zlomky; tedy součin nezáleží na pořadí jeho činitelů: \[ n \cdot \frac{km}{n} = km = k \left( n \cdot \frac{m}{n} \right) = n \cdot k \cdot \frac{m}{n}. \] Porovnáním levé a pravé strany dojdeme k závěru, že výsledkem je celé číslo $km$ rozdělené na $n$ dílů: \[ k \cdot \frac{m}{n} = \frac{km}{n}. \]
Další otázkou je, jakou hodnotu dostaneme, když vynásobíme dva zlomky, např. $\frac{m}{n}$ a $\frac{k}{\ell}$? Podobným způsobem odvodíme, že dostaneme takovou hodnotu, která po přenásobení celým číslem $n\ell$ bude rovna celému číslu $m k$: \[ (n\ell) \cdot \left( \frac{m}{n} \cdot \frac{k}{\ell} \right ) = n \cdot \frac{m}{n} \cdot \ell \frac{k}{\ell} = mk = (n\ell) \frac{mk}{n\ell} \] Všimněme si, že $n\ell \neq 0$. <!-- Obě odpovědi jsou dány tím, že chceme, aby násobení racionálních čísel bylo ve stejném duchu jako násobení celých čísel. -->
Budeme-li celek dělit právě na jednu část, dostaneme opět onu část, tedy \[ \frac{m}{1} = 1 \cdot \frac{m}{1} = m. \] Tím jsme objevili mezi novými hodnotami celá čísla.
Podobně jako jsme si odvodili vlastnosti výše lze odvodit i další dvě vlastnosti. Nové hodnoty mají i uspořádání, které je kompatibilní s uspořádáním celých čísel: \[ \frac{m}{n} < \frac{k}{\ell} \quad \Longleftrightarrow \quad m\ell < kn. \] Další vlastností je podmínka, kdy se dva zlomky rovnají: \[ \frac{m}{n} = \frac{k}{\ell} \quad \Longleftrightarrow \quad m\ell = kn. \] Opět tedy máme kompatibilitu s celými čísly. Zároveň se na povrch dostala technická vlastnost zlomků a to sice jejich nejednoznačnost. Vidíme totiž, že \[ \frac{m}{n} = \frac{m}{n} \cdot \frac{s}{s} = \frac{ms}{ns}. \] Pokud bychom chtěli jednoznačný zápis, můžeme čísla $m$ a $n$ volit nesoudělná: dostaneme tak zlomek ve zkráceném tvaru.
A co sčítání zlomků? Kolik je $\frac{m}{n} + \frac{k}{\ell}$? Chovejme se ke zlomkům opět jako k celým číslům a pokusme se je sečíst tak, že součet vynásobíme $1$ zapsanou jako $\frac{n \ell}{1} \cdot \frac{1}{n \ell}$. Dostaneme \[ \begin{split} \left ( \frac{m}{n} + \frac{k}{\ell} \right) \cdot \frac{n \ell}{1} \cdot \frac{1}{n \ell} = \left ( \frac{m n \ell }{n} + \frac{k n \ell}{\ell} \right) \cdot \frac{1}{n \ell} = \left ( \frac{m \ell }{1} + \frac{k n }{1} \right) \cdot \frac{1}{n \ell} \\ = \left ( m \ell k n \right) \cdot \frac{1}{n \ell} = \left ( \frac{m \ell + k n }{1} \right) \cdot \frac{1}{n \ell} = \frac{m \ell + k n }{n \ell}. \end{split} \] Poněkud formálnější cestou se tedy dostaneme ke známému společnému jmenovateli $n\ell$, který nám zjednodušené říká, na jak malé díly je třeba celek dělit, aby se oba dva jmenovatelé $n$ a $\ell$ do něj svými díly „vešly“.
Pro úplnost upozorněme na to, že v našem formálním odvození jsme mimo násobení použili také kompatibilitu sčítání a násobení - distributivní zákon.
Množina racionálních čísel je množina všech zlomků: \[ \Q = \left \{ \frac{m}{n} \colon m,n \in \Z, n > 0 \right\}, \] kde $\Z$ značí množinu celých čísel. Typické značení $\Q$ pochází s německého slova poměr - der Quotient.
Uvedeme si také formální konstrukci racionálních čísel.
Formální konstrukce racionálních čísel
Na konstrukci racionálních čísel lze nahlížet jako na obecnější koncept. K získání tohoto konceptu potřebujeme extrahovat všechny potřebné vlastnosti, které nám z množiny celých čísel umožnily vytvořit množinu racionálních čísel. Těmito abstraktními vlastnostmi a strukturami, které mají tyto vlastnosti, se zabývá *obecná algebra*. Z pohledu obecné algebry jsou celá čísla oborem integrity: množinou, která je vybavena abstraktními operacemi sčítáním a násobením s požadovanými vlastnostmi, a která neobsahuje tzv. dělitele nuly. Dělitelem nuly nazveme takové nenulové číslo $x$, k němuž existuje nenulový kamarád $y$, se kterým po vynásobení vyjde nula, tedy $xy=0$.
Mezi vlastnostmi oboru integrity není záruka možnosti provádět zobrazení inverzní k násobení - dělení. Pokud prvky dělit umíme, takovému objektu se říká *těleso*. (Samozřejmě, nedělí se prvkem, který hraje roli čísla $0$. )
Těleso, které vznikne z oboru integrity přidáním minimálního počtu prvků tak, aby bylo možné dělit, se nazývá *podílové těleso*, nebo také těleso zlomků. V případě konstrukce racionálních čísel vede výroba podílového tělesa nejprve na kartézský součin $\Z$ a $\Z \setminus \{ 0 \}$, kde první složka hraje roli čitatele, druhá jmenovatele. Tento kartézský součin je třeba dále faktorizovat na třídy ekvivalence, abychom se zbavili nejednoznačnosti zápisu hodnot zlomků.
Mohutnost množiny racionálních čísel
O kolik je $\Q$ větší než $\Z$? Naše intuice říká, že množina racionálních čísel je větší než množina celých čísel - přece jsme v podstatě vyráběli nové hodnoty. Správný závěr z relace $\Z \subset \Q$ by měl být, že $\Q$ není menší než $\Z$.
Jak vlastně měříme počet prvků nekonečných množin? Nekonečné množiny mezi sebou můžeme pouze porovnávat a to sestrojováním zobrazení, které nám jednoznačně přiřadí dva prvky z obou množin k sobě. Jednoznačnost je v pojmech zobrazení dána prostotou - injektivitou.
Ideální je, podaří-li se nám najít přímo bijektivní zobrazení, tedy tzv. zobrazení 1 ku 1. Pak můžeme o nekonečných množinách prohlásit, že mají stejnou mohutnost, což je termín, který zobecňuje počet prvků. Jak je to tedy s $\Q$ a $\Z$? Umíme mezi nimi najít bijekci?
Odpověď je ano, a tedy ačkoliv jsme přidávali prvky, nevznikne množina, která by byla v tomto smyslu větší.
Jak takovou bijekci najít? Stačí najít nějaké seřazení prvků $\Q$. To nám umožní prvkům přiřadit celočíselné indexy, což je hledaná bijekce. Možných seřazení je mnoho, kladné zlomky lze například seřadit nejprve podle hodnoty součtu čitatele a jmenovatele, čímž vzniknou konečné množiny, a ty už jednotlivě seřadíme snadno. Tím vzniknou indexy pro kladné zlomky, záporné seřadíme symetricky a máme vyhráno.
My si ukážeme ještě jiný přístup. Jelikož $\Z \subset \Q$, pak nutně existuje injektivní zobrazení ze $\Z$ do $\Q$. Zobrazení dané předpisem \[ \frac{m}{n} \mapsto 2^m3^n \] je injektivním zobrazením z $\Q$ do $\Z$ (a to i pokud budeme brát soudělná $m$ a $n$). Máme tedy dvě prostá zobrazení $\Z \to \Q$ a $\Q \to \Z$. Existence těchto dvou prostých zobrazení „tam a zpět“ je postačující podmínkou pro existenci bijekce. Tento fakt je známý jako Cantorova-Bernsteinova věta.
O nekonečné množině, kterou lze bijektivně zobrazit na celá čísla, říkáme, že je spočetná. (Místo celých čísel se v definici spočetnosti často uvádí přirozená čísla. Čtenář si sám laskavě rozmyslí, že celá i přirozená čísla lze mezi sebou taktéž bijektivně zobrazit a odpustí nám, že jsme tuto otázku nechali otevřenou.)
Iracionální čísla
Jak již sám název napovídá, iracionální čísla jsou ta čísla, která nejsou racionální. Čísly se myslí takzvaná reálná čísla, která můžeme najít v našem světe, když budeme například měřit vzdálenosti. Stačí nám měřit vzdálenosti od námi zvoleného bodu pojmenovaného číslem $0$ na nějaké přímce. Body na přímce tedy identifikujeme s jejich vzdáleností od bodu $0$. Pro bod $0$ nám tedy volba sedí.
Zvolme si na přímce další bod, jiný než $0$, který bude představovat hodnotu $1$ (a tedy i jeho jméno bude $1$). Tím si nastavíme náš metr pro další hodnoty: tento metr umíme kopírovat do obou stran a nalézt na přímce všechna celá čísla. Díky tomu nalezneme také všechna racionální čísla. Konkrétně bod $\frac{m}{n}$ nalezneme tak, že úsečku omezenou body $0$ a $m$ rozdělíme na $n$ stejně dlouhých úseček a $\frac{m}{n}$ je krajní bod nejblíže k nule.
Nás bude zajímat spíše opačná otázka. Máme-li nějaký bod $b$ na přímce, představuje nějaké racionální číslo? Pokud existuje celé číslo $n$ takové, že když za sebe položíme $n$ kopií úsečky omezené bodem $0$ a $b$, a dostaneme se tam do bodu $m \in \Z$ (to umíme změřit), pak platí $b = \frac{m}{n}$. Když se nám takové $n$ nepodaří najít (tedy vyzkoušíme-li všechny), pak jsme našli neracionální hodnotu - iracionální číslo.
Jak se přesvědčíme, že se to vůbec může stát? Představme si čtverec nakreslený v rovině, o hraně délky $1$. (Ten můžeme vyrobit pomocí našeho metru a kružítka.) Pojďme měřit délku jeho úhlopříčky. Označme ji $d$. (Pomocí kružítka nalezneme bod $d$ na naší přímce.) Na pomoc pozveme Pythagora, který zajásá a řekne nám, že \[ d^2 = d \cdot d = 1 \cdot 1 + 1 \cdot 1 = 2. \] Důkaz provedeme sporem. Předpokládejme, že $d$ je racionální číslo. Musí tedy existovat nesoudělná celá čísla $m$ a $n$ taková, že platí \[ d = \frac{m}{n}. \] Pak ovšem musí platit \[ 2 = d^2 = \frac{m^2}{n^2} \] a tedy \[ 2 n^2 = m^2. \] Z toho plyne, že $m$ je sudé a můžeme jej zapsat jako $m = 2t$. Dostaneme $2 n^2 = m^2 = 4t^2$ a následně \[ n^2 = 2t^2. \] Tedy $n$ je také sudé. To ovšem není možné, protože $n$ a $m$ jsou nesoudělná. Nás předpoklad, že $d$ je racionální, je tedy mylný.
Závěr je, že existuje vzdálenost, kterou nelze popsat racionální hodnotou.
Odmocniny a další iracionální hodnoty
Podobně jako číslo $\sqrt{2}$ bychom rychle zjistili, že každé číslo $\sqrt[q]{d}$ pro $q \geq 1$, které není celé, je iracionální. Tím jsme objevili mnoho dalších iracionálních hodnot. A jejich sčítáním a násobením můžeme objevit ještě dalších mnoho nových iracionálních hodnot.
Kolik iracionálních čísel tedy existuje? Je jich jistě nekonečně mnoho, ale jedná se o spočetnou množinu?
A existují nějaká iracionální čísla, která se nedají vyjádřit násobením a sčítáním odmocnin?
Podívejme se nejprve na způsob reprezentace reálných čísel.
Reprezentace hodnot v číselných soustavách
Vraťme se zpět k naší úsečce o délce $1$. Všechny racionální hodnoty, které na ní jsou, umíme poznat a umíme je i označit. Rádi bychom nyní označili i všechny zbylé hodnoty. K tomuto použijeme tzv. *číselnou soustavu*, která nám umožní jednoznačným způsobem všechny hodnoty identifikovat. Poznačme $x$ číslo, které chceme pojmenovat - najít jeho reprezentaci v daném systému. Omezíme se na interval $\langle 0,1)$, tedy $0 \leq x < 1$. Tento interval si pokryjeme $N$ disjunktními intervaly takto: \[ \langle 0,1) = \bigcup_{i=1}^N \langle c_{i-1}, c_i), \] kde $c_0 = 0$, $c_N = 1$ a $c_i < c_{i+1}$. Abychom byli schopni s těmito hodnotami pracovat, tak si zvolíme $c_i \in \Q$. Tyto disjuktní intervaly nám definují vybraný číselný systém.
V prvním kroku se koukneme, do kterého z těchto $N$ intervalů číslo $x$ padne. Padne jen do jednoho, tedy $x \in \langle c_{j_0}, c_{{j_0}+1} )$ pro právě jedno $j_0$. Index $j_0$ bude prvním symbolem hledané reprezentace čísla $x$.
Dalším krok zahájíme tím, že si bod $c_{j_0}$ přejmenujeme na $0$ a bod $c_{{j_0}+1}$ na $1$. Tím nám vznikne nová úsečka o délce $1$. Původní bod $x$ bude na této úsečce ležet, pouze vzhledem k ní bude mít jinou hodnotu, kterou označíme $x_1$. Platí, že $x_1 = \frac{x - c_{ j_0 } } { c_{ { j_0 } + 1 } - c_{ j_0 } }$. S tímto nově získaným číslem budeme opakovat předchozí postup (s novou jednotkovou úsečkou) a získáme tak další symbol do reprezentace čísla $x$, který označíme $j_1$.
Tento postup budeme opakovat: nalezenme $x_2$, získáme $j_2$, ... Celkově tedy máme algoritmus pro získání posloupnosti s členy z $\{0,\ldots,N-1\}$, která nám jednoznačně identifikuje číslo z intervalu $\langle 0,1)$: \[ \left ( j_i \right )_{i=0}^{+\infty}. \]
Následující obrázek ilustruje několik prvních kroků tohoto algoritmu pro konkrétní volbu číselného systému.
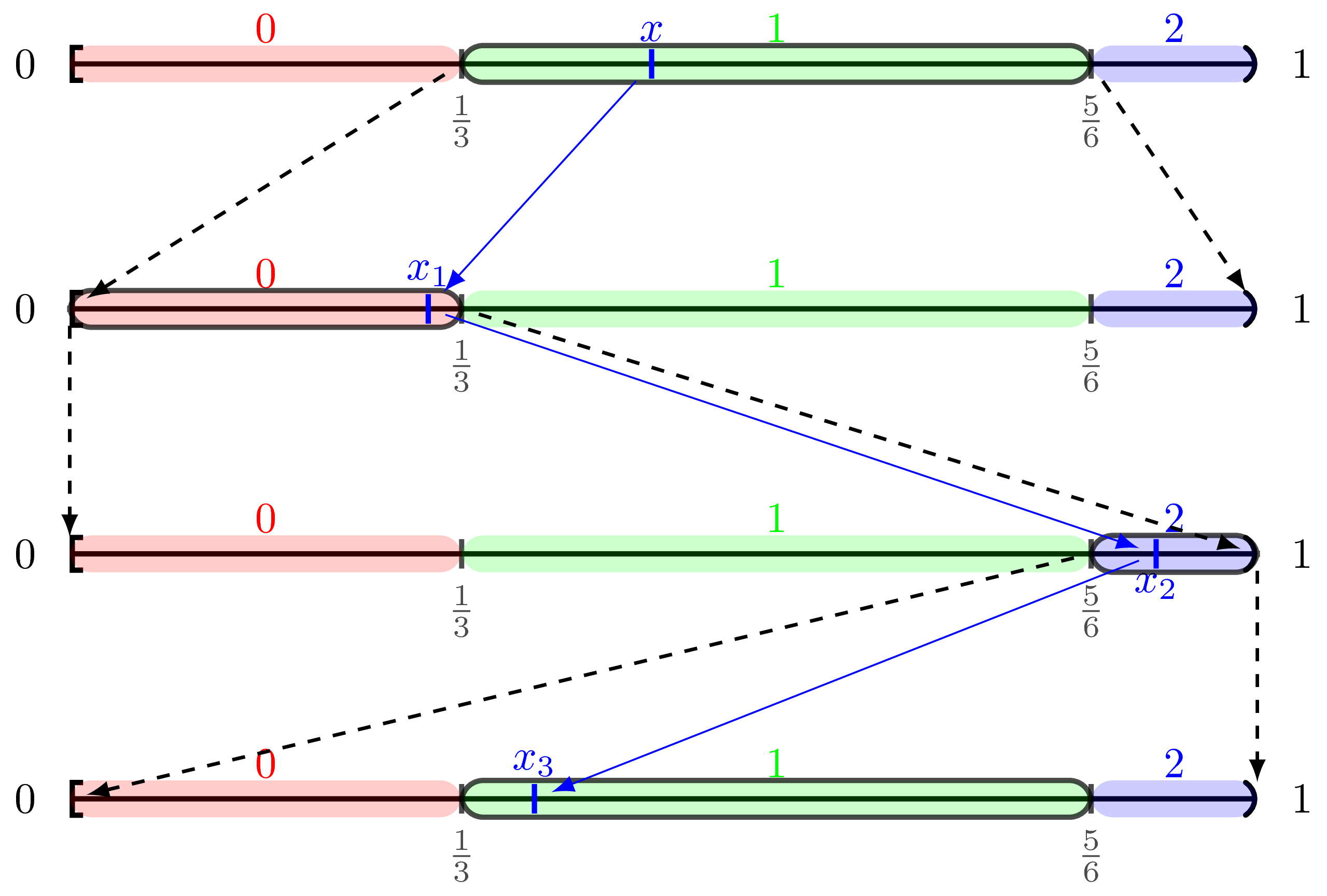
Obrázek č. 3: Ilustrace hledaní reprezentace čísel v číselné soustavě s $N = 3$, $c_1 = \frac{1}{3}$ a $c_2 = \frac{5}{6}$. Začátek reprezentance čísla $x$ je ${\color{green}1}{\color{red}{0}}{\color{blue}{2}}{\color{green}{1}}\ldots$
Proč nám hodnotu identifikuje reprezentace jednoznačně? Z našeho postupu lze odvodit, že \[ x = c_{j_0} + (c_{{j_0}+1} - c_{j_0})^{-1} \left ( c_{j_1} + (c_{{j_1}+1} - c_{j_1})^{-1} \left ( c_{j_2} + \ldots \right) \right), \] kde oblíbený „třítečkový operátor“ je zjednodušeným zápisem pro limitu v tomto smyslu: $x = \lim_{k \to +\infty} \sum_{i=0}^k \frac{ c_{j_i} }{ \prod_{t=0}^{i-1} (c_{ {j_t} +1} - c_{ j_t }) }$. Lze odvodit, že všechny možné reprezentace jsou bijektivně zobrazeny na interval $\langle 0, 1)$. Zdůrazněme, že všechny možné reprezentace nejsou to samé, jako všechny možné posloupnosti ze symbolů $\{0,1,\ldots,9\}$. Tedy pokud mají $x$ a $x'$ stejnou reprezentaci $(j_i)_{i=0}^{+\infty}$, potom nutně $x=x'$.
Poznamenejme dále, že opustit interval $\langle 0, 1)$ není složité a že výše popsaný algoritmus se obvykle zastavuje v okamžik, kdy je jasné, že naše posloupnost bude pokračovat už jen samými nulami.
Pojďme k velmi obvyklé volbě reprezentace, a to sice $N = 10$ a $c_i = \frac{i}{10}$. Postupem uvedeným výše pak získáme reprezentaci všech čísel z intervalu $\langle 0, 1)$ v desítkové soustavě. Výraz pro hodnotu čísla $x$ se díky volbě stejné délky pro všechny podintervaly změní na \[ x = \sum_{i=0}^{+\infty} c_{j_i} 10^{-i} = \sum_{i=0}^{+\infty} j_i 10^{-i-1}, \] kde druhá rovnost je dána vhodnou volbou indexů.
Důležité je všimnout si opačné strany pohledu. Zvolíme-li si v námi vybraném systému reprezentace nějakou posloupnost, pak této posloupnosti lze stejným vzorcem přiřadit nějakou hodnotu. Dokonce existují volby posloupností, které povedou na stejnou hodnotu. Tato nejednoznačnost ovšem vznikne jedině tak, že budeme mít posloupnost jejíž členy jsou od nějakého místa pouze cifry $9$.
Přirozenou otázkou je, jak konkrétně najít reprezentaci například $\sqrt{2}$ v desítkové soustavě. Na to jsme odpověď nedali. Jen víme, že to lze. Na otázku kolik je všech iracionálních čísel nám naše úvahy výše postačí.
Předpokládejme, že reálných čísel je spočetně mnoho. Můžeme je tedy seřadit a všem číslům dát indexy $1, 2, \ldots$. Mějme tedy jedno takové seřazení a od každého čísla mějme jeho reprezentaci v desítkové soustavě. Najdeme číslo, které v našem seznamu není, a to následujícím způsobem. Pro číslo na indexu $i$ se koukneme na pozici $i$ v jeho desítkové reprezentaci. Nalezneme tam nějakou hodnotu $d_i \in \{0,1,2, \ldots, 9\}$. Vybereme libovolnou jinou hodnotu z této množiny mimo $9$, označíme ji $d_i'$. Číslo dané posloupností $\left ( d_i' \right)$ v našem seřazeném seznamu není: pozici $i$ má s $i$-tým číslem odlišnou. Tím, že jsme se vyhnuli cifrám $9$, jsme zajistili, že posloupnost $\left ( d_i' \right)$ je reprezentací nějakého čísla. (Tento krok ve skutečnosti není nutný v takové míře, je ale názornější.) Jelikož reprezentace jsou jednoznačné, dojdeme ke sporu, a tedy náš předpoklad, že množina reálných čísel je spočetná, je mylný. Protože racionální čísla jsou spočetnou podmnožinou reálných čísel, pak iracionální čísla nemohou být spočetné. (Sjednocení dvou spočetných množin je taktéž spočetné.)
Tedy iracionálních čísel je ve smyslu bijektivních zobrazení více než racionálních čísel. Zapisováním hodnot ve tvaru zlomku jsme tedy mnoho hodnot vynechali!
Dále se podíváme na pravděpodobně nejslavnější iracionální číslo, které je jiného typu než číslo $\sqrt{2}$.
Číslo $\pi$
Ludolfovo číslo, téměř výlučně značené $\pi$, je poměr obvodu kružnice a jejího průměru. Jedná se o konstantu, tedy nezáleží jakou kružnici nakreslíme, poměr jejího obvodu a průměru bude vždy stejný. Se základními znalostmi analýzy si lze toto tvrzení dokázat. Do kružnice vepíšeme pravidelné $n$-úhelníky. Jejich obvod, který umíme jednoduše spočítat, nám dává dolní odhad obvodu kružnice. Pro $n = 3,4,5$ tuto situaci znázorňuje následující obrázek:
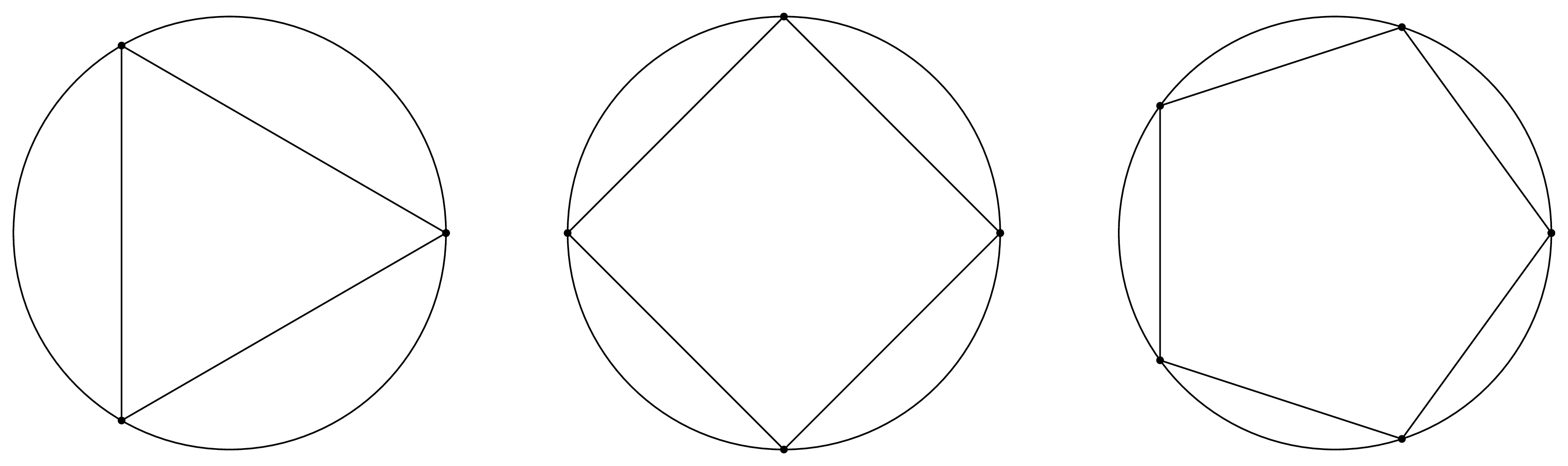
Obrázek č. 4: Vepsané pravidelné $n$-úhelníky do kružnice.
Tento dolní odhad bude nezávislý na velikosti průměru kružnice. Abychom dostali samotný obvod kružnice, je třeba provést limitní přechod $n \to +\infty$. Jelikož jsou ale odhady nezávislé na průměru pro všechna $n$, je nezávislá i samotná limita.
Jak již bylo napsáno výše, číslo $\pi$ je iracionální. Tento dobře známý fakt již nemá tak přímočarý důkaz. Navíc se jedná o číslo, které je *transcendentní*. To znamená, že není kořenem žádného polynomu s celočíselnými koeficienty. Z tohoto pohledu se jedná o jiný druh iracionálního čísla než je číslo $\sqrt{2}$, které transcendentní není (je kořenem polynomu $x^2-2$).
Hodnotu $\pi$ tedy umíme vyčíslit pouze v nějaké přesnosti: známe konečný počet prvků jeho reprezentace (a máme algoritmus jak počítat další). V desítkové soustavě je přibližná hodnota $\pi$ často $3{,}14$. Nicméně svět, ve kterém je poměr obvodu a průměru kružnice roven $3{,}14$ není ten náš - rovina v tomto světě se nechová jako ta naše a na nakreslení kružnice potřebuje o trochu méně inkoustu než v tom našem. Těžko si představit, jaké by to mělo další důsledky (a příčiny).
Zdánlivá nepraktičnost iracionality čísla $\pi$ sem tam na světě někoho trápí. Asi nejznámějším je pokus o uzákonění hodnoty $\pi$.
Číslo $\mathrm e$
Základ přirozeného logaritmu, Eulerovo číslo $\mathrm e$, je taktéž častým příkladem iracionálního čísla. Jedná se taktéž o číslo trascendentní. Pro zahuštění atmosféry si jeho iracionalitu dokážeme.
Nejprve si vyslovíme pomocné tvrzení: nechť $\alpha$ je reálné číslo. Pokud existuje posloupnost párů celých čísel $(x_n,y_n)$, kde $y_n > 0$, $\frac{x_n}{y_n} \neq \alpha$ a $\lim_{n \to +\infty} \left | x_n - \alpha y_n \right | = 0$, potom $\alpha$ je iracionální.
Pomocné tvrzení ponecháme bez důkazu a požádáme o laskavého čtenáře o důkaz vlastní (důkaz sporem je velmi názorný). Pro důkaz iracionality $\mathrm e$ vyjdeme z definice Eulerova čísla \[ \mathrm{e} = \sum_{k=0}^{+\infty} \frac{1}{k!}. \] Dále použijeme pomocné tvrzení pro $x_n = n!$ a $y_n = n! \sum_{k=0}{n}\frac{1}{k!}$. Dostaneme \[ \left | x_n - \mathrm{e} y_n \right | = n! \sum_{k=n+1}^{+\infty} \frac{1}{k!}. \] A tedy \[ \begin{split} 0 < \left | x_n - \mathrm{e} y_n \right | & = \frac{1}{n+1} + \frac{1}{(n+1)(n+2)} + \frac{1}{(n+1)(n+2)(n+3)} + \ldots \\ & < \frac{1}{n+1} + \frac{1}{(n+1)^2} + \frac{1}{(n+1)^3} + \ldots \\ & = \frac{1}{n}. \end{split} \] Tedy $\lim_{n \to +\infty} \left | x_n - \alpha y_n \right | = 0$, a tedy z pomocného tvrzení plyne, že číslo $\mathrm e$ je iracionální.
Další vlastnosti
Každé iracionální číslo je limitou posloupnosti racionálních čísel. Tedy každé iracionální číslo lze dostatečně dobře aproximovat nějakým racionálním číslem. Naopak, pokud vezmeme všechna racionální čísla, z nich všechny možné posloupnosti a jejich limity, pak dostaneme všechna reálná čísla. Tomuto procesu se obecně říká zúplnění.
O dalších vlastnostech iracionálních čísel, především různých jejich aproximací, napíšeme v dalším příspěvku Iracionální čísla a jejich aproximace.
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).

