Iracionální čísla a jejich aproximace
Štěpán Starosta, publikován 31. 10. 2017, editován 26. 10. 2018
Popíšeme základní teoretický přístup k definici aproximace nějakého čísla. Velmi krátce představíme metody hledání aproximací a uvedeme i míru aproximovatelnosti iracionálního čísla. Zmíníme několik zajímavých vlastností Lagrangeova spektra, které souvisí s různou aproximovatelností všech reálných čísel.
$\DeclareMathOperator{\fl}{fl} \newcommand\Fl[1]{\fl \left ( #1 \right)}$
V příspěvku o iracionálních číslech jsme se zabývali tím, co to vlastně iracionální čísla jsou. V tomto příspěvku se budeme zabývat hledáním přibližných hodnot iracionálních čísel. Problém nalezení přibližné hodnoty daného iracionálního reálného čísla je možná stejně starý jako objevení prvního iracionálního čísla. Tento objev se datuje kolem roku $-500$ po Kristu. V termínech řecké filozofie je nutné se bavit spíše o pojmu nepoměřitelnosti namísto mladšího pojmu iracionalita. Historicky zvídavý čtenář se může obrátit např. na [1].
Přibližná hodnota iracionálního čísla nám pomůže alespoň nepřesně umístit hodnotu na číslenou osu a porovnat ji s jinými hodnotami, kterým zcela rozumíme: racionálními čísly. Tato problematika se obecně nazývá diofantickou aproximací. Diofantos, podle kterého se tato oblast matematiky jmenuje, žil ve 3. století. Jedná se o živou a velmi obsáhlou doménu, o které bylo napsáno mnoho knih, např. [3]
My se nejprve podíváme na nejjednoduší aproximace iracionálních čísel, poté se koukneme na klasické aproximace pomocí řetězových zlomků a dostaneme se až k míře iracinality.
Aproximace reálných čísel
Schopnost umět spočítat přibližné hodnoty iracionálních čísel je dnes nutnost. Počítače, které nám umožňují provádět masivní výpočty často musí pracovat jen s přibližnými hodnotami: v paměti mají daný prostor pro několik prvních cifer z binárního rozvoje používaného čísla (více detailů k této tématice si lze přečíst v příspěvku Základní potíže při práci s čísly s plovoucí čárkou).
Použití několika prvních cifer z poziční reprezentace čísla, ať už o bázi dva, deset či jiného celého čísla, se samozřejmě řadí mezi aproximace pomocí racionálních čísel. V diofantické aproximaci se často hledá nejlepší aproximace za určitých podmínek. Tyto podmínky jsou stanoveny ukotvením maximální hodnoty jmenovatele zlomku, který bude aproximovat. Tedy pro aproximované číslo $\alpha \in \R$ hledáme číslo $\frac{p}{q} \in \Q$ takové, že \[ \left | \alpha - \frac{p}{q} \right| < \left| \alpha - \frac{p'}{q'} \right| \] pro všechna $\frac{p'}{q'} \in \Q$ různá od $\frac{p}{q}$ s podmínkou $0 < q' \leq q$. Této aproximaci se také říká aproximace prvního druhu.
Pojďme se podívat, jak vypadají tyto aproximace pro nějaké iracionální číslo. Několik prvních aproximací aproximací prvního druhu pro $\sqrt{2}$ jsou tyto:
\[ 1, \frac{3}{2}, \frac{4}{3}, \frac{7}{5}, \frac{17}{12}, \frac{24}{17}, \frac{41}{29}, \frac{99}{70}, \frac{140}{99} \ldots \]
K aproximaci prvního druhu přirozeně patří aproximace druhého druhu, která neměří pouze vzdálenost mezi aproximací a číslem, ale ještě penalizuje vzdálenost velikostí jmenovatele, který jsme na racionální aproximaci použili. Je definována obdobně jako aproximace prvního druhu: pro aproximované číslo $\alpha \in \R$ hledáme číslo $\frac{p}{q} \in \Q$ takové, že \[ q \left | \alpha - \frac{p}{q} \right| < q' \left| \alpha - \frac{p'}{q'} \right| \] pro všechna $\frac{p'}{q'} \in \Q$ různá od $\frac{p}{q}$ s podmínkou $0 < q' \leq q$. Všimněme si, že tato upravená podmínka na racionální aproximaci je přísnější v následujícím smyslu: je-li nějaké číslo aproximací druhého druhu, pak je aproximací prvního druhu.
Naopak neplatí, že by aproximace prvního druhu musela být i aproximací druhého druhu. Ukažme si toto názorně uvedením aproximací druhého druhu pro $\sqrt{2}$:
\[ 1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \frac{99}{70}, \frac{239}{169}, \frac{577}{408}, \frac{1393}{985}, \frac{3363}{2378}, \ldots \]
K aproximacím druhého druhu se vrátíme níže v části o řetězových zlomcích. Předtím se ještě podíváme na ukázky metod získávání aproximací reálných čísel. Obě výše uvedené definice nejsou nijak konstruktivní: není totiž jasné, jaké jmenovatele správně volit. Co je horší, pokud bychom chtěli hrubou silou hledat nějakou takovou dobrou aproximaci, budeme potřebovat velmi často ještě lepší aproximaci našeho čísla, abychom prokázali, že naše aproximace je prvního nebo druhého druhu. To samozřejmě postrádá dobrý smysl. Přibližné hodnoty pro praktické použití se tedy hledají jinak.
Uveďme tzv. babylonskou metodu pro výpočet aproximace čísla $\sqrt{2}$. Mějme $x_0 \in \R$ a definujme posloupost $(x_i)$ rekurzivně takto: \[ x_{n+1} = \frac{1}{2} \left ( x_n + \frac{d}{x_n} \right ). \] Potom platí, že limita této posloupnosti je $\sqrt{d}$ a navíc s každou další napočítanou hodnotou jsme k $\sqrt{d}$ blíže než předtím. Tedy chceme-li dosáhnout nějaké přesnosti dané například počtem desetinných míst, stačí počítat a čekat, až se nám na daném desetinném místě hodnota ustálí. Pojďme toto zkusit opět pro $\sqrt{2}$:
| $i$ | $x_i$ |
|---|---|
| 0 | 1.00000000000000 |
| 1 | 1.50000000000000 |
| 2 | 1.41666666666667 |
| 3 | 1.41421568627451 |
| 4 | 1.41421356237469 |
| 5 | 1.41421356237310 |
| 6 | 1.41421356237310 |
| 7 | 1.41421356237310 |
| 8 | 1.41421356237310 |
| 9 | 1.41421356237310 |
| 10 | 1.41421356237310 |
Tato metoda, jak její název napovídá, je velmi stará. Pro vysvětlení, proč metoda funguje doporučujeme https://en.wikipedia.org/wiki/Methods_of_computing_square_roots či [2]. Ve zkratce a termínech novější matematiky je tato metoda Newtonovou metodou pro funkci $f(x) = x^2 - d$. Popis této a jiných metod naleznete v příspěvku Numerické hledání řešení rovnic.
Hledání takovýchto vzorců, které účinně napočítávají přibližné hodnoty, má již dlouho tradici a nachází uplatnění zvláště v době různých počítacích strojů, kde se takové algoritmy hodí. Jako ukázku toho, jak se v kontextu dnešních počítačů napočítavají přibližné hodnoty doporučujeme příspěvek o implementaci funkce sinus.
Pro představu, kolik úsilí bylo při hledání přibližných hodnot různých iracionálních čísel, doporučujeme přehled metod pro výpočet aproximací čísla $\pi$.
Vraťme se nyní k důležitému pojmu z teorie diofantických aproximací, a to k řětězovým zlomkům.
Řetězové zlomky
Řetězové zlomky lze chápat jako způsob reprezentace hodnoty reálného čísla, stejně tak jako desítková soustava. Máme-li číslo $\alpha \in \R$, pak o posloupnosti $(a_i)$, kde $a_0 \in \Z$ a $a_i \in \N$ řekneme, že je řetězovým zlomkem čísla $\alpha$ pokud platí \[ \alpha = a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+\cfrac{1}{a_3+\cdots}}}. \] Obvykle tento fakt značíme $\alpha = [a_0, a_1, a_2, a_3, \ldots]$. Posloupnost $(a_i)$ může být jak konečná, tak nekonečná. Platí, že konečná je právě tehdy, když je $\alpha$ racionální. Nás tedy zajímají nekonečné posloupnosti.
Jak lze získat reprezentaci nějakého čísla $\alpha$ v této soustavě? Prvním krokem je $a_0 = \lfloor \alpha \rfloor$. V dalším kroku si poznačíme $\xi_1 = \frac{1}{ \alpha - a_0 }$ a spočteme $a_1 = \lfloor xi_1 \rfloor$. Takto pokračujeme dále: \[ \xi_{i+1} = \frac{1}{\xi_i - a_i} \quad \text{ a } \quad a_{i+1} = \lfloor \xi_{i+1} \rfloor, \] pokud nenarazíme na $\xi_{i+1} = 0$, což se stane pouze a právě pro $\alpha \in \Q$. Více o řetězových zlomcích např. v klasickém spisku [4].
Spočtěme řetězový zlomek čísla $\sqrt{2}$. Prvním koeficientem je jistě $1$, protože $\lfloor \sqrt{2} \rfloor = 1$. Další koeficient je roven \[ \lfloor \frac{1}{\sqrt{2}-1} \rfloor = \lfloor \frac{\sqrt{2}+1}{1} \rfloor = 2. \] Pro třetí koeficient tedy vyjde \[ \lfloor \frac{1}{\sqrt{2}+1-2} \rfloor = \lfloor \frac{1}{\sqrt{2}+1} \rfloor, \] což jsme viděli již v předchozím kroku. Tím pádem jsou všechny zbývající koeficienty rovny $2$. Celkem tedy zjišťujeme, že řetězový zlomek čísla $\sqrt{2}$ je $[1,2,2,2,2,2,\ldots]$
Souvislost aproximací a řetězových zlomků je dána sblíženými zlomky. Sblížený zlomek k číslu $\alpha$ je racionální číslo, jehož řetězový zlomek vznikne z nějakého konečného začátku řetězového zlomku $\alpha$. Uveďme konkrétní příklad pro $\sqrt{2}$:
| řetězový zlomek | hodnota |
|---|---|
| $ [1] $ | $ 1 $ |
| $ [1, 2] $ | $ \frac{3}{2} $ |
| $ [1, 2, 2] $ | $ \frac{7}{5} $ |
| $ [1, 2, 2, 2] $ | $ \frac{17}{12} $ |
| $ [1, 2, 2, 2, 2] $ | $ \frac{41}{29} $ |
| $ [1, 2, 2, 2, 2, 2] $ | $ \frac{99}{70} $ |
| $ [1, 2, 2, 2, 2, 2, 2] $ | $ \frac{239}{169} $ |
| $ [1, 2, 2, 2, 2, 2, 2, 2] $ | $ \frac{577}{408} $ |
| $ [1, 2, 2, 2, 2, 2, 2, 2, 2] $ | $ \frac{1393}{985} $ |
| $ [1, 2, 2, 2, 2, 2, 2, 2, 2, 2] $ | $ \frac{3363}{2378} $ |
Není náhodou, že tyto hodnoty jsme již viděli v seznamu výše, protože každý sblížený zlomek je aproximací druhého druhu a zároven každá aproximace druhého druhu je sblíženým zlomkem. Pokud bychom chtěli postihnout všechny aproximace prvního druhu, museli bychom zavést ještě další pojem „semisblíženého“ zlomku a reprezentace aproximovaného čísla řětězovým zlomkem by nám dala odpověď.
Řetězové zlomky mají velmi úzkou souvislost i pokud aproximace s jmenovatelem $q$ začneme poměřovat s $\frac{1}{q^2}$. Platí, že pokud pro iracionální $\alpha$ a nesoudělné $p$ a $q$ platí \[ \left | \alpha - \frac{p}{q} \right | \leq \frac{1}{2 q^2}, \] pak $\frac{p}{q}$ je sblížený zlomek čísla $\alpha$. I v tomto smyslu jsou tedy řetězové zlomky nejlepšími aproximacemi čísla $\alpha$.
Míra aproximovatelnosti
Vyvstává otázka, pro jaký faktor u $\frac{1}{q^2}$ na pravé straně budeme schopni vždy najít nekonečně mnoho nesoudělných $p$ a $q$. Pro $\frac{1}{2}$ tomu tak je. Nejlepší takovou mez udává Hurwitzova věta: pro $\alpha$ iracionální existuje nekonečně mnoho nesoudělných $p$ a $q$ takových, že \[ \left | \alpha - \frac{p}{q} \right | \leq \frac{1}{\sqrt{5} q^2}. \] Mez je nejlepší v tom smyslu, že zaměníme-li faktor $\frac{1}{\sqrt{5}}$ za cokoliv menšího, tvrzení neplatí. Elegantní důkaz této slavné věty lze nalézt v [5].
Jedno z čísel, pro které tvrzení neplatí, je zlatý řez, neboli $\frac{\sqrt{5}+1}{2}$. Řetězový zlomek zlatého řezu sestává ze samých jedniček, tedy $\frac{\sqrt{5}+1}{2} = [1,1,1,1,\ldots]$. Pokud vynecháme čísla, jejichž řětězový zlomek končí na samé jedničky, můžeme naši mez posunout. Je-li $\alpha$ iracionální číslo, jehož řetězový zlomek nekončí samými jedničkami, pak existuje nekonečně mnoho nesoudělných $p$ a $q$ takových, že \[ \left | \alpha - \frac{p}{q} \right | \leq \frac{1}{\sqrt{8} q^2}. \]
Pro iracionální $\alpha$ si tuto mez můžeme dobře definovat následujícím způsobem: \[ \mu(\alpha) = \inf \left \{ c > 0 \colon \text{ existuje nekonečně mnoho nesoudělných } p,q \text{ tak, že } \left | \alpha - \frac{p}{q} \right | \leq \frac{c}{q^2} \right \}. \] Číslu $\mu(alpha)$ (někteří autoři definují inverzní hodnoty) se někdy říká Markovova konstanta čísla $\alpha$.
Hodnota $\mu(\alpha)$ nám tedy vyjadřuje jakousi míru aproximovatelnosti reálného čísla. Pokud $\mu(\alpha) = 0$, pak řekneme, že $\alpha$ je dobře aproximovatelné číslo. Platí, že číslo je dobře aproximovatelné přávě tehdy, když jsou prvky jeho řetězového zlomku neomezené. Špatně aproximovatelná čísla mají tedy omezené prvky řetězového zlomku.
Naši rozpravu ukončíme krátkým popisem zajímavé množiny, které vznikne z prozkoumání všech možných hodnot $\mu(\alpha)$: \[ L = \{ \mu(\alpha) \colon \alpha \in \R \}. \] Této množině se říká Langrageovo spektrum. Z výše popsaného plyne, že $L \subset \langle 0 , \frac{1}{\sqrt{5}} \rangle$. Další hodnotou, která v $L$ je, je $\frac{1}{\sqrt{8}}$. Obdobně narazíme na 3. největší hodnotu v $L$ a tou je $\frac{5}{\sqrt{221}}$. Tato diskrétní část spektra končí u největší hromadné hodnoty v $L$, kterou je $\frac{1}{3}$. Zbytek zajímavého chování $L$ je naznačen na následujícím obrázku. Výchozím bodem pro další informace o Lagrangeově spektru je kniha [6].
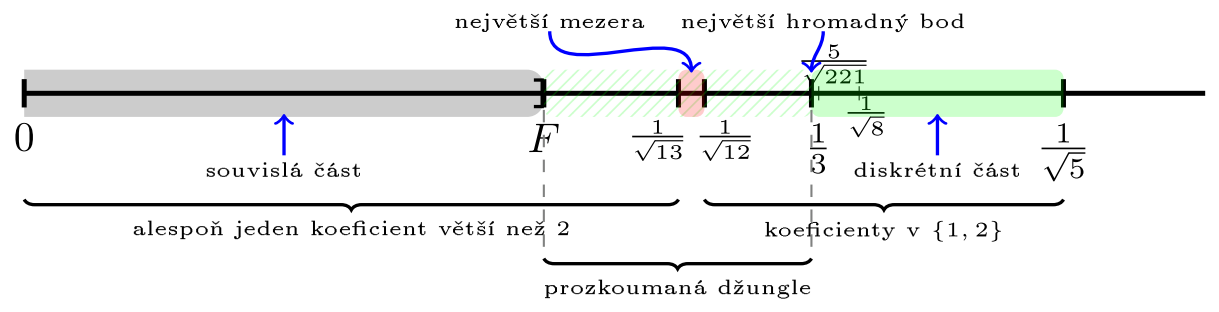
Obrázek č. 1: Lagrangeovo spektrum. Největší hodnoty tvoří diskrétní část, jejichž nejmenší hodnota je největším hromadným bodem $\frac{1}{3}$. Nejmenší hodnoty tvoří naopak souvislou část $\langle 0, F \rangle$, kde $F = \frac{555391024-70937 \sqrt{462}}{2507812168} \approx 0.22$ (Freimanova konstanta). Souvislé části se také říká „Hall's ray“. Mezi diskrétní a souvislou částí je oblast označená jako prozkoumaná džungle. Tato část obsahuje různé izolované body, intervaly a mezery. Největší mezera je naznačena na obrázku. Tato největší mezera zároveň udává, jaké koeficienty jsou v řetězovém zlomku čísla, jehož Markovovu konstantu zobrazujeme.
Použitá literatura
- Kurt Von Fritz. The Discovery of Incommensurability by Hippasus of Metapontum, Annals of Mathematics, Second Series, Vol. 46, No. 2 (Apr., 1945), pp. 242-264, http://www.jstor.org/stable/1969021.
- Olga Kosheleva. Babylonian method of computing the square root: Justifications based on fuzzy techniques and on computational complexity, NAFIPS 2009, Annual Meeting of the North American Fuzzy Information Processing Society, Cincinnati, OH, 2009, pp. 1-6. DOI: 10.1109/NAFIPS.2009.5156463.
- Wolfgang M. Schmidt. Diophantine Approximations and Diophantine Equations, Springer Berlin Heidelberg, 1991. DOI: 10.1007/bfb0098246.
- A. Ya. Khinchin. Continued Fractions, Dover Publications; Revised edition (May 14, 1997). ISBN-10: 0486696308.
- J. H. E. Cohn. Hurwitz' theorem, Proc. Amer. Math. Soc. 38 (1973), 436. DOI: 10.1090/S0002-9939-1973-0313195-9.
- Thomas W. Cusick, Mary E. Flahive. The Markoff and Lagrange Spectra, American Mathematical Society, 1989. ISBN 978-0-8218-1531-1.
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).

