Numerické hledání řešení rovnic
Jak řešit rovnice, které neumíme vyřešit na papíře? Ukážeme si několik iterativních postupů pro hledání kořenů reálných funkcí jedné reálné proměnné. Metody porovnáme a zmíníme se i o několika zajímavých problémech vedoucích na tento typ úlohy.
Popis problému
Základní pojmy
Při studiu středoškolské matematiky čtenář již jistě narazil na problém řešení rovnice typu \begin{equation}\label{eq-f} f(x) = 0 \end{equation} v neznámé $x$, kde $f$ je zadaná reálná funkce reálné proměnné případně závisející na dalších parametrech. Řešením úlohy \eqref{eq-f} pak nazýváme číslo $x_*$, které splňuje $f(x_*) = 0$. O $x_*$ se také mluví jako o kořenu funkce $f$. Řešení této úlohy může být nekonečně mnoho, konečně mnoho, nebo i žádné.
Známé řešitelné příklady
Zcela jistě čtenář umí nalézt řešení kvadratické rovnice \[ ax^2 + bx + c = 0 \] s parametry $a,b,c$ a ví, že
- pokud $b^2 - 4ac = 0$, pak má tato rovnice právě jedno řešení $x = -\frac{b}{2a}$,
- pokud $b^2 - 4ac > 0$, pak má tato rovnice právě dvě řešení $x_\pm = \frac{1}{2a}\left( -b \pm \sqrt{b^2 - 4ac} \right),$
- pokud $b^2 - 4ac < 0$, pak nemá žádné řešení v reálném oboru (má ovšem dvě komplexní řešení).
Rovnice \[ \sin(x) = 1 \] má nekonečně mnoho řešení \[ x_k = \pi k, \quad k \in \mathbb{Z}. \]
Naproti tomu rovnice \[ \sin^2 (x) + 1 = 0 \] nemá ani jedno řešení. Výraz na levé straně je vždy větší nebo roven $1$ a nikdy (pro žádné reálné $x$) tak nemůže být nulový.
Obecný problém
Ve středoškolské matematice se v drtivé většině případů setkáváte s příklady rovnic $f(x) = 0$, které umíte explicitně vyřešit podobně jako ve výše uvedených příkladech. To ovšem ve studentech zanechává poněkud nesprávný dojem, že umí řešit rovnice tohoto typu. Opak je pravdou. Explicitní řešení lze nalézt typicky jenom u školních příkladů.
V mnoha a mnoha zajímavých příkladech (pár ukázek nabídneme čtenáři níže) nejsme schopni takovéto explicitní řešení nalézt. I přesto bychom chtěli danou rovnici alespoň v rámci jisté přesnosti vyřešit. Je to možné?
V tomto článku si nejprve ukážeme několik tzv. numerických (přibližných) algoritmů pro hledání řešení zadaných rovnic pomocí počítače. Poté si ukažme zajímavé příklady, kde nám středoškolské kuchařky pro řešení různých typů rovnic (trigonometrické, exponenciální, polynomiální) budou platné jako mrtvému zimník.
Základní metody pro hledání nulových bodů funkcí
Soustřeďme se nyní na řešení úlohy nalézt řešení rovnice \[ f(x) = 0, \] kde $f$ je předem daná reálná funkce reálné proměnné. O této funkci předpokládáme, že je definována na jistém intervalu $J$.
Následující metody ukazují různé strategie, jak se snažit hledat řešení uvedené rovnice (o kterém v tento moment ani nevíme jestli existuje). Každá z metod může na různých příkladech vykazovat různé výsledky. Zdůrazněme, že se soustředíme na hledání alespoň jednoho řešení. Nezabýváme se otázkou, jak nalézt všechny, je-li jich více. Bez hlubší analýzy funkce $f$ a znalosti jejích vlastností toho nelze příliš mnoho tvrdit.
Bisekce (půlení)
Vstupem této metody jsou dva body (čísla) $a_0$ a $b_0$, $a_0 < b_0$, z intervalu $J$. Funkční hodnoty funkce $f$ v bodech $a_0$ a $b_0$ jsou nenulové (jinak jsme úlohu vyřešili) a mají různé znaménko. Tuto podmínku můžeme elegantně vyjádřit požadavkem, aby $f(a_0) \cdot f(b_0) < 0$.
Nyní uvažme bod $c$ uprostřed mezi $a_0$ a $b_0$, tj. \[ c = \frac{a_0 + b_0}{2}. \] Pokud náhodou (to se typicky nestane) $f(c) = 0$, pak jsme úlohu vyřešili. Pokud tato situace nenastala, pak $f(c)$ je buď kladné nebo záporné. To znamená, že buď $f(a_0)$ a $f(c)$ mají různá znaménka, nebo $f(c)$ a $f(b_0)$ mají různá znaménka. V prvním případě položíme $a_1 := a_0$ a $b_1 := c$, ve druhém pak $a_1 := c$ a $b_1 = b_0$. Tato situace je graficky znázorněna na následujícím obrázku:
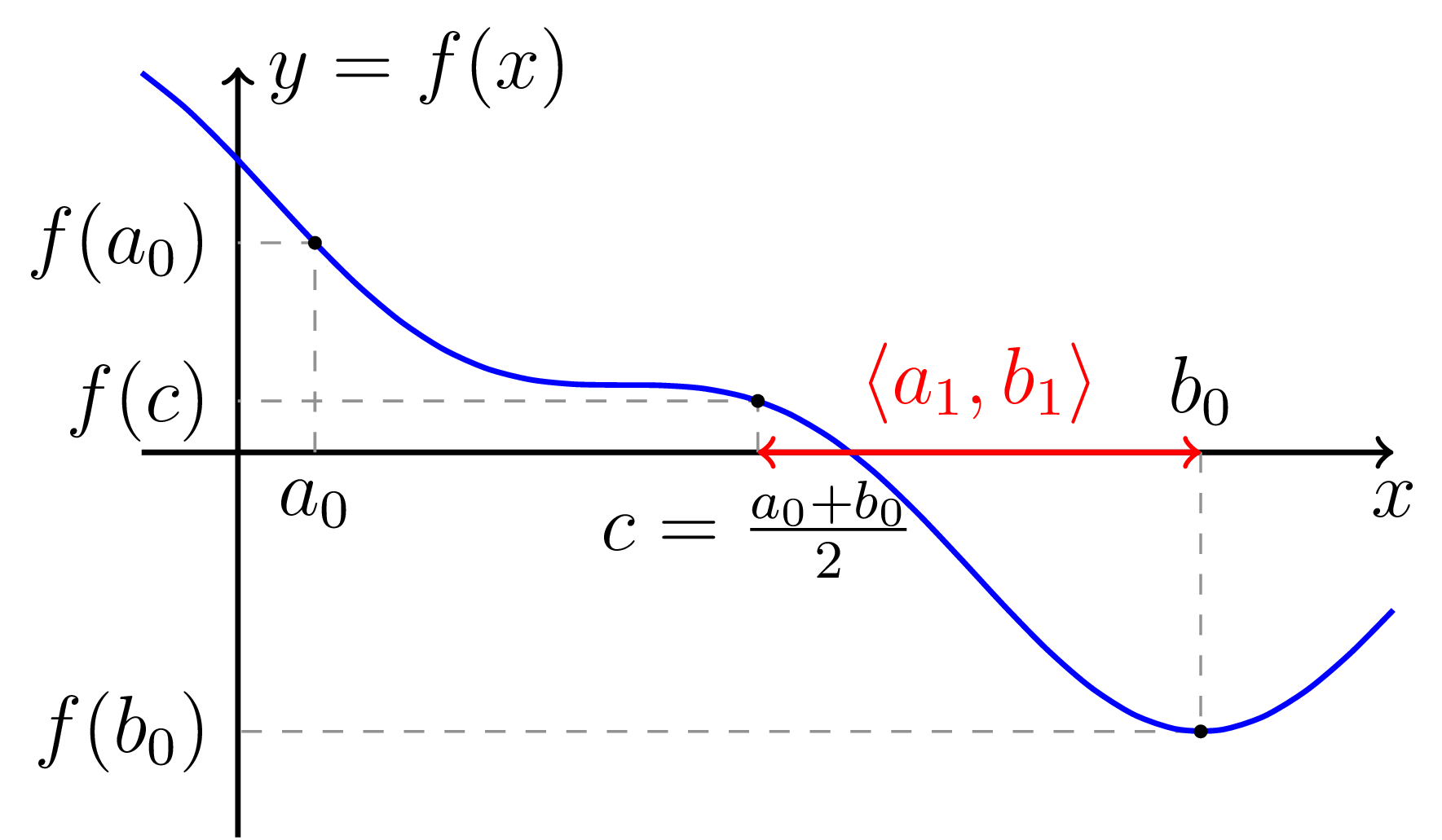
Obrázek č. 1: Znázornění principu bisekční metody pro hledání řešení rovnice $f(x) = 0$. Začneme s intervalem $\langle a_0, b_0 \rangle$ majícím na krajích různá znaménka funkčních hodnot a vybereme půlku tohoto intervalu $\langle a_1, b_1 \rangle$ tak, aby znaménka funkčních hodnot byla stále různá.
Dále celý proces opakujeme s $a_1$ a $b_1$ místo $a_0$ a $b_0$ a tak dále. Tím získáváme posloupnosti $(a_n)_{n=1}^\infty$ a $(b_n)_{n=1}^\infty$, pro něž platí (skutečně, v každém kroku nový krajní bod leží uprostřed starých krajních bodů) \[ 0 < b_n - a_n = \frac{b-a}{2^{n}}. \] V případě, že jsme se v některém z kroků prostředním bodem trefili do kořene funkce $f$, tak je již úloha vyřešena (viz popis kroku algoritmu, resp. konstrukce bodu $c$, výše). Obě posloupnosti jsou navíc monotónní a konvergují ke stejné limitě $x_*$. Tento bod, $x_*$, leží v každém z intervalů $\langle a_n, b_n \rangle \subset \langle a,b \rangle$. Pokud je funkce $f$ navíc spojitá, pak lze ukázat, že $x_*$ splňuje $f(x_*) = 0$ a je tedy námi hledaným řešení původního problému.
Podstatnou výhodou této metody je její konvergence a kontrola chyby. Body které konstruujeme se neustále přibližují z obou stran k hledanému řešení.
Nevýhodou této metody je její relativně pomalá rychlost konvergence. Konkrétní ukázku nalezne čtenář na konci tohoto článku.
Regula falsi
Princip této metody je stejný jako u metody bisekce. Jediným rozdílem je způsob volby dělícího bodu intervalu. Bisekce ho volí uprostřed daného intervalu, regula falsi k tomu účelu využívá lineární interpolaci funkce $f$ na daném intervalu.
Mějme tedy opět zadány dva body $a_0 < b_0$ v intervalu $J$ a předpokládejme opět různost znamének $f(a_0)$ a $f(b_0)$. Lineární interpolací mezi body $(a_0, f(a_0))$ a $(b_0, f(b_0))$ je přímka s rovnicí \[ y = \frac{f(b_0) - f(a_0)}{b_0 - a_0} (x - a_0) + f(a_0). \] Tato přímka protíná osu $x$ v bodě $(c,0)$. Po přímočarých algebraických úpravách toto $c$ snadno spočteme, \[ c = \frac{a_0 f(b_0) - b_0 f(a_0)}{f(b_0) - f(a_0)}. \] Dále pokračujeme jako u metody bisekce. Tedy na základě hodnoty $f(c)$ buď hledání ukončíme, nebo klademe $a_1 = a_0$ a $b_1 = c$ pokud $f(a_0) \cdot f(c) < 0$, nebo $a_1 = c$ a $b_1 = b_0$ pokud $f(c) \cdot f(b_0) < 0$. Pro ilustraci uvádíme obrázek.
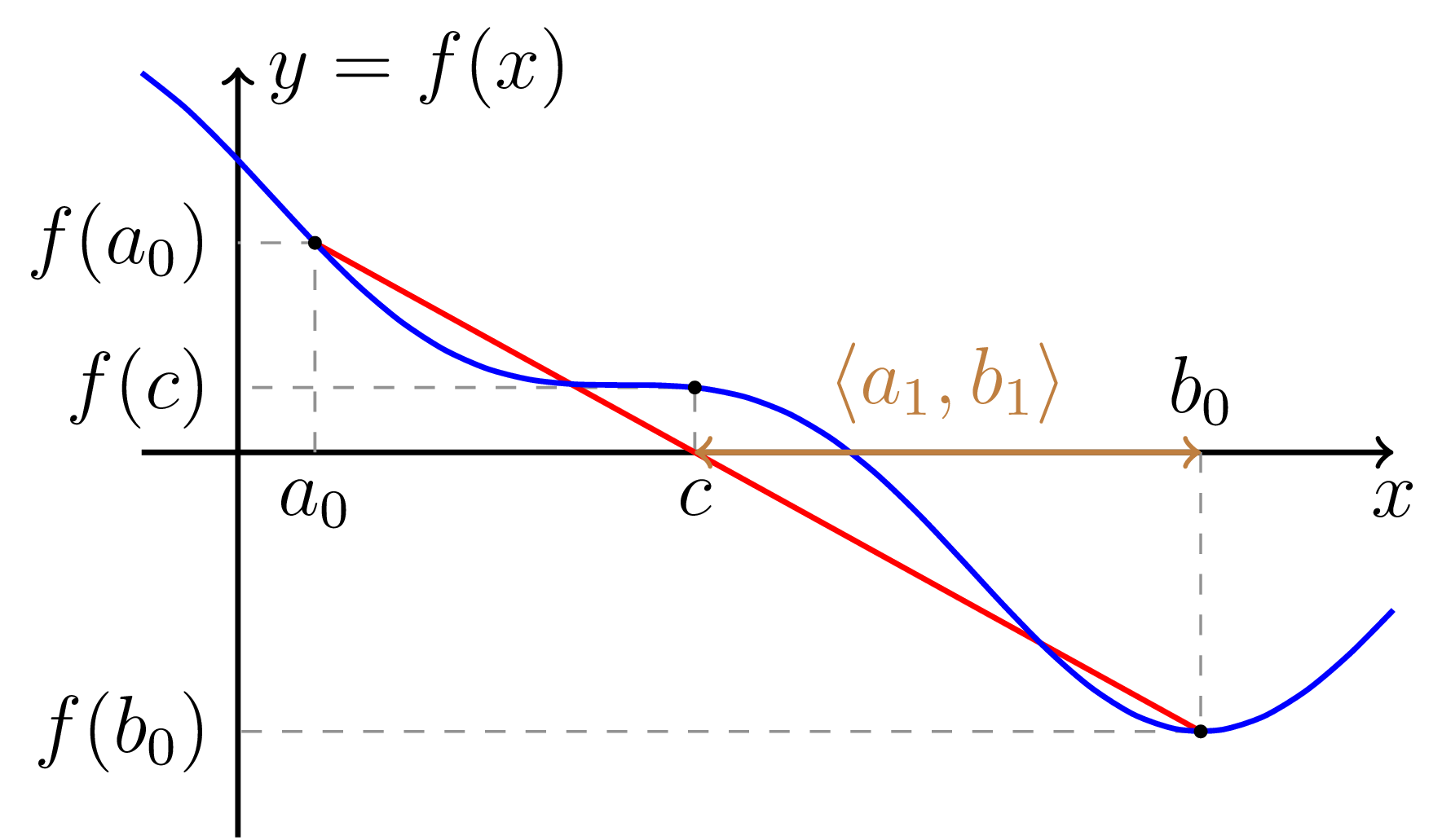
Obrázek č. 2: Znázornění principu metody regula falsi pro hledání řešení rovnice $f(x) = 0$. Začneme s intervalem $\langle a_0, b_0 \rangle$ majícím na krajích různá znaménka funkčních hodnot. Interval rozdělíme pomocí lineární interpolace funkce (znázorněna červenou barvou) a vybereme část tohoto intervalu $\langle a_1, b_1 \rangle$ tak, aby znaménka funkčních hodnot byla stále různá.
Regula falsi má podobné vlastnosti jako metoda bisekce. Za předpokladu spojitosti funkce $f$ a různosti znamének funkčních hodnot na krajích intervalu je konvergentní a řešení leží v počátečním intervalu. Konvergenci lze očekávat o něco rychlejší než v případě bisekce.
Newtonova metoda
Tato metoda vyžaduje vyhodnocování nejen funkčních hodnot funkce $f$, ale i její derivace $f'$. K vylepšení aproximace řešení rovnice $f(x) = 0$ totiž použijeme tečnu ke grafu funkce $f$. Uživatel tedy musí derivaci zadat, nebo bychom ji museli odhadovat (touto komplikovanější variantou se zde zabývat nebudeme; navíc lze v tomto případě použít metodu sečny uvedenou vzápětí). Dále máme na vstupu zadán jeden bod $a_0$ představující první aproximaci řešení naší úlohy.
Nejprve sestrojíme tečnu grafu funkce $f$ v bodě $(a_0, f(a_0))$. Tato tečna je přímka daná rovnicí \[ y = f'(a_0) (x - a_0) + f(a_0). \] Průsečík této přímky s osou $x$ je dán vzorcem (za předpokladu nenulovosti $f'(a_0)$) \begin{equation}\label{eq-dif-newton} a_1 := a_0 - \frac{f(a_0)}{f'(a_0)}. \end{equation} Nyní tento proces opakujeme s $a_1$ místo $a_0$.
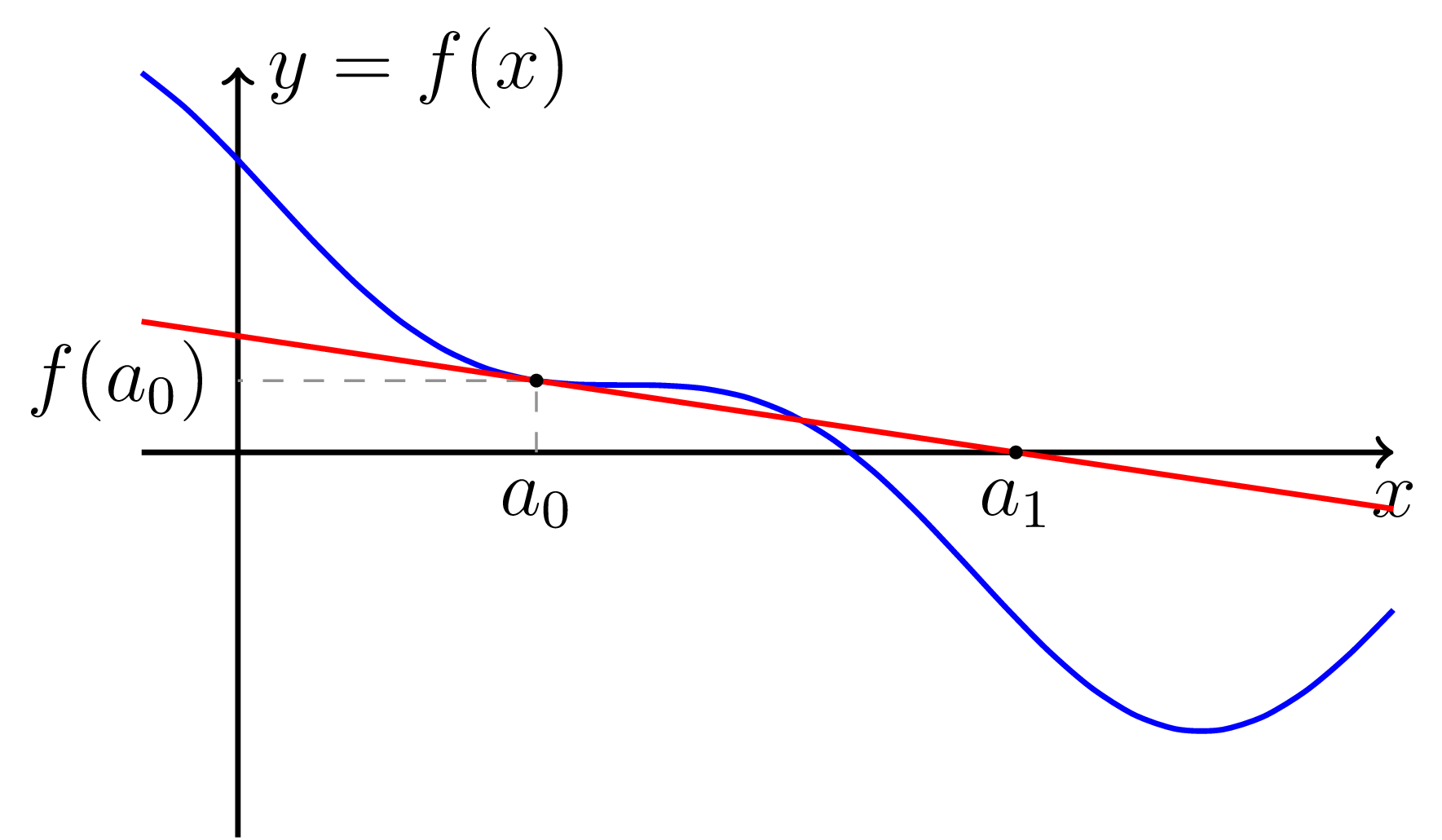
Obrázek č. 3: Znázornění principu Newtonovy metody pro hledání řešení rovnice $f(x) = 0$. Aproximaci řešení $a_0$ se snažíme vylepšit posunutím do průsečíku $(a_1,0)$ tečny ke grafu funkce $f$ v bodě $(a_0,f(a_0))$ (znázorněna červenou barvou) s osou $x$.
Tímto způsobem se pokoušíme zkonstruovat posloupnost $(a_n)_{n=0}^\infty$, o které doufáme, že konverguje k hledanému řešení úlohy $f(x) = 0$.
Newtonova metoda trpí několika neduhy. Algoritmus konstrukce této posloupnosti může selhat, například pokud derivace ve jmenovateli rekurentního vzorce je nulová (či velmi blízká nule v rámci pracovní přesnosti), nebo když průsečík tečny s osou $x$ padne mimo definiční obor naší funkce. Konvergence posloupnosti není zaručena. Přímo z konstrukce členů posloupnosti $(a_n)_{n=0}^\infty$ neplyne žádná možnost jejich kontroly. Lze zkonstruovat případy, kdy zkonstruovaná posloupnost konverguje nebo je dokonce periodická.
Optimisticky lze ale říci, že začneme-li s prvním bodem $a_0$ blízko skutečného řešení, pak Newtonova metoda konverguje velmi rychle. Viz praktické ukázky níže.
Metoda sečny
Metoda sečny je variace Newtonovy metody pro funkce $f$, které nejsou diferencovatelné, nebo pro které nemáme možnost počítat derivaci (uživatel ji nezadal nebo je funkce zadána tak komplikovaně, že není jednoduché spočítat její derivaci), či je to výpočetně výrazně náročnější než vyhodnocení funkční hodnoty. Místo tečny v Newtonově metodě použijeme sečnu.
Na vstupu je tedy zadána funkce $f$ a dva body $a_0$ a $b_0$. Sestrojíme sečnu grafu funkce $f$ procházející body $(a_0, f(a_0))$ a $(b_0, f(b_0))$. Tato přímka je dána rovnicí \[ y = \frac{f(b_0) - f(a_0)}{b_0 - a_0} (x - b_0) + f(b_0). \] Průsečíkem této přímky s osou $x$ je bod $(c, 0)$, kde \begin{equation}\label{eq-dif-secna} c = b_0 - \frac{b_0 - a_0}{f(b_0) - f(a_0)} f(b_0). \end{equation} Položíme $b_1 := c$ a $a_1 := b_0$ a celý proces opakujeme s $a_1, b_1$ místo $a_0, b_0$.
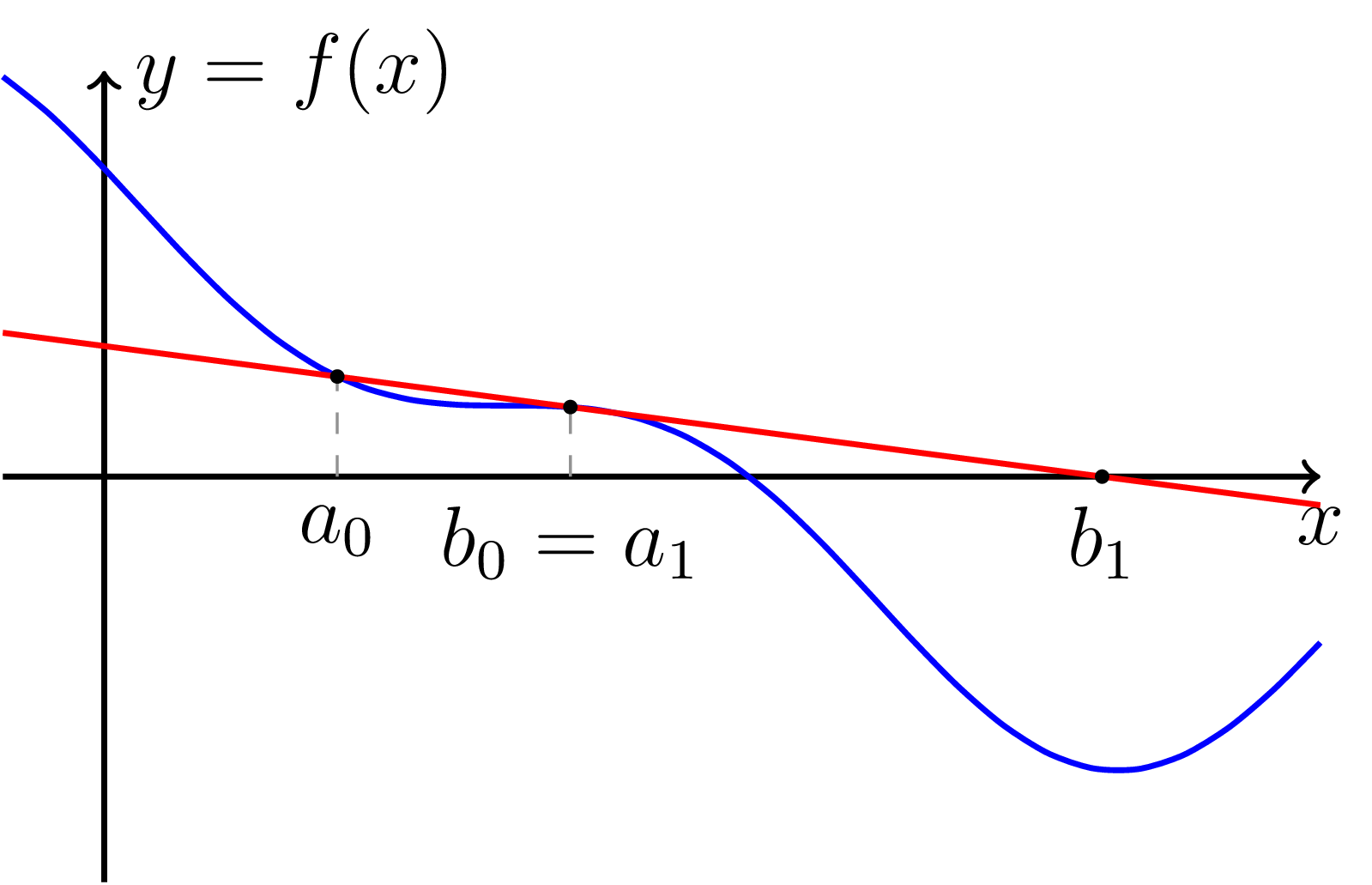
Obrázek č. 4: Znázornění principu metody sečny pro hledání řešení rovnice $f(x) = 0$. Sečna je znázorněna červeně.
U této metody si sice pamatujeme dva body, ale na rozdíl od metody bisekce a regula falsi hledané řešení neleží nutně mezi nimi. Jedná se vlastně o diskrétní variantu Newtonovy metody (derivaci v ní nahrazujeme diferencí, porovnejte rovnici \eqref{eq-dif-newton} a \eqref{eq-dif-secna}).
I u této metody nemáme přílišnou kontrolu nad chováním zkonstruované posloupnosti. Obecně o ní platí podobné poznámky jako v případě Newtonovy metody.
Kritérium pro zastavení
V praktické implementaci nelze výše uvedené metody provádět až do nekonečna (všechny čtyři metody dávají nekonečné posloupnosti, o kterých doufáme, že konvergují k hledanému řešení).
Je nutné výpočet ve vhodný okamžik ukončit, jinak jsme pouze implementovali nekonečnou smyčku. K zastavení lze použít například následující kritéria:
- pokud pro poslední aproximaci řešení, ozn. $c$, je $|f(c)|$ dostatečně malé (typicky závisí na zvolené přesnosti výpočtu),
- u bisekce a regula falsi lze skončit pokud poslední sestrojený interval $(a,b)$ je dostatečně krátký.
Dále bývá dobrým zvykem v implementaci algoritmu nastavit jistý maximální povolený počet iterací. Pokud do tohoto maximálního počtu iterací nedosáhneme zastavovací podmínky, pak vrátíme chybu a ohlásíme selhání pokusu o nalezení řešení.
Příklady použití
Naplňování nádrží (*Water filling*)
Představme si, že máme $n$ vzájemně propojených nádrží s dny v různých výškách a různými plochami den. Dále máme zadáno množství vody, které do systému vpustíme. Otázkou je, jak vysoko se vyrovná hladina vody v nádržích. Alternativně lze o této úloze uvažovat jako o optimalizační úloze, při níž se snažíme rovnoměrně distribuovat jistou veličinu mezi různě zatížené a různě kapacitní kanály (pro jednoduchost se budeme držet vodní interpretace, ve které ale není úplně jednoduché si představit vzájemné propojení kanálů: trubky je spojující jsou zavedeny vždy u dna nádrže a objem vody v trubkách zanedbáváme). Popisovaná situace je znázorněna na obrázku 5.
Nechť je tedy zadáno $n \in \mathbb{N}$ nezáporných konstant $\alpha_1, \dots, \alpha_n \geq 0$. Tyto konstanty reprezentují jak vysoko jsou dna nádrží umístěna (viz obrázek 5). Dále nechť je zadáno $n$ kladných konstant $\beta_1, \dots, \beta_n > 0$. Tyto konstanty reprezentují obsah podstav nádrží. Do soustavy napustíme vodu o objemu $V > 0$ a ptáme se na jaké hladině $h \geq 0$ se voda vyrovná a jak bude v jednotlivých nádržích.
Je-li hladina ve výšce $h$, pak v $i$té nádrži je \[ \beta_i \cdot \max(0,\, h - \alpha_i) \] vody. Rozeberme toto tvrzení podrobněji. Funkce $\max$ vrací větší z obou jejích argumentů. Výraz výše je nulový pokud je dno výše než hladina (výraz $h - \alpha_i$ je pak záporný). V opačném případě kdy $h - \alpha_i \geq 0$ představuje hloubku vodního sloupce v $i$té nádrži a přenásobením $\beta_i$ získáme objem vody v této nádrži.
Hledaná hladina $h$ proto musí splňovat \[ \sum_{i=1}^n \beta_i \cdot \max(0,\, h - \alpha_i) = V. \] Alternativně, $h$ je řešením rovnice \begin{equation}\label{eq-wf} g(h) := V - \sum_{i=1}^n \beta_i \cdot \max(0,\, h - \alpha_i) = 0 \end{equation} Povšimněme si, že $g(0) = V$ a $\lim_{h\to\infty} g(h) = -\infty$. Funkce $g$ je navíc klesající a spojitá. Úloha \eqref{eq-wf} má tedy právě jedno řešení, které můžeme nalézt vhodně zvolenou numerickou metodou. Na následujícím obrázku je znázorněna jedna konkrétně zvolená situace.
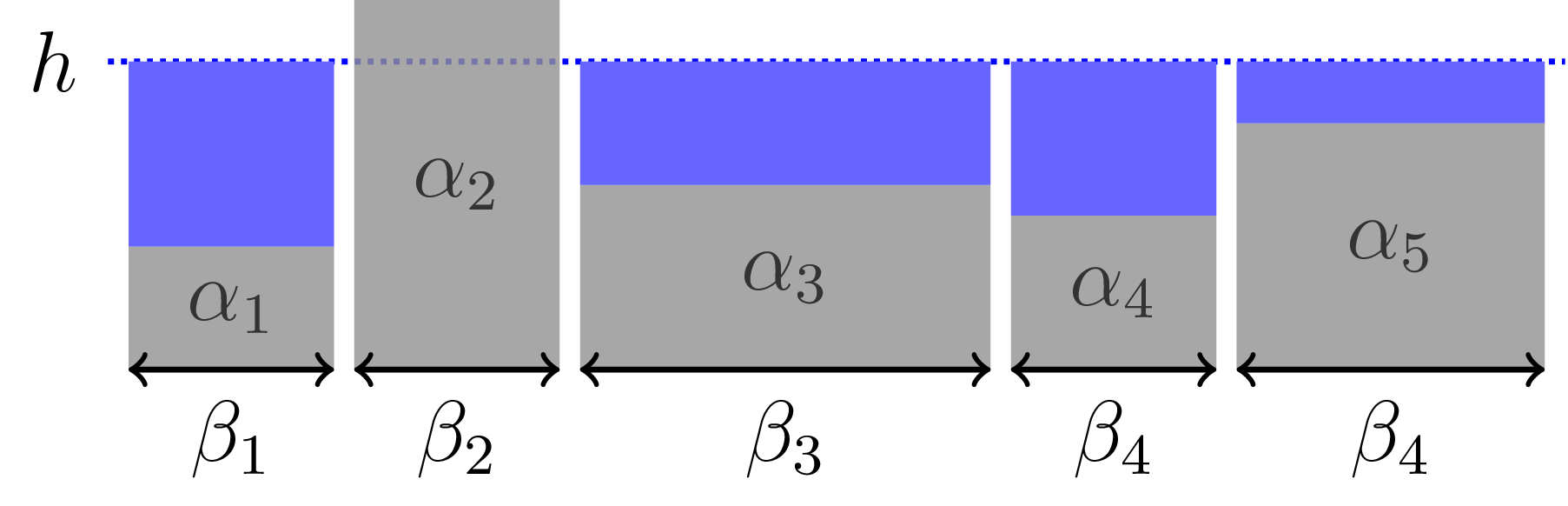
Obrázek č. 5: Ilustrace a řešení problému naplňování nádrží s pěti nádržemi a $\beta_1 = \beta_2 = \beta_4 = 1$, $\beta_3 = 2$, $\beta_5 = \frac{3}{2}$, $\alpha = \frac{1}{5}$, $\beta_2 = \frac{3}{5}$, $\beta_3 = \frac{3}{10}$, $\beta_4 = \frac{1}{4}$, $\beta_5 = \frac{3}{2}$ a $V = \frac{11}{10}$. Pomocí metody sečny s počátečním $a_0 = 0$ a $b_0 = \frac{22}{10}$ ve čtyřech iteracích najdeme $h = \frac{1}{2}$ s přesností $10^{-16}$.
Pro zajímavost uveďme graf funkce $g$ z konkrétního příkladu uvedeného v předchozím obrázku 5.
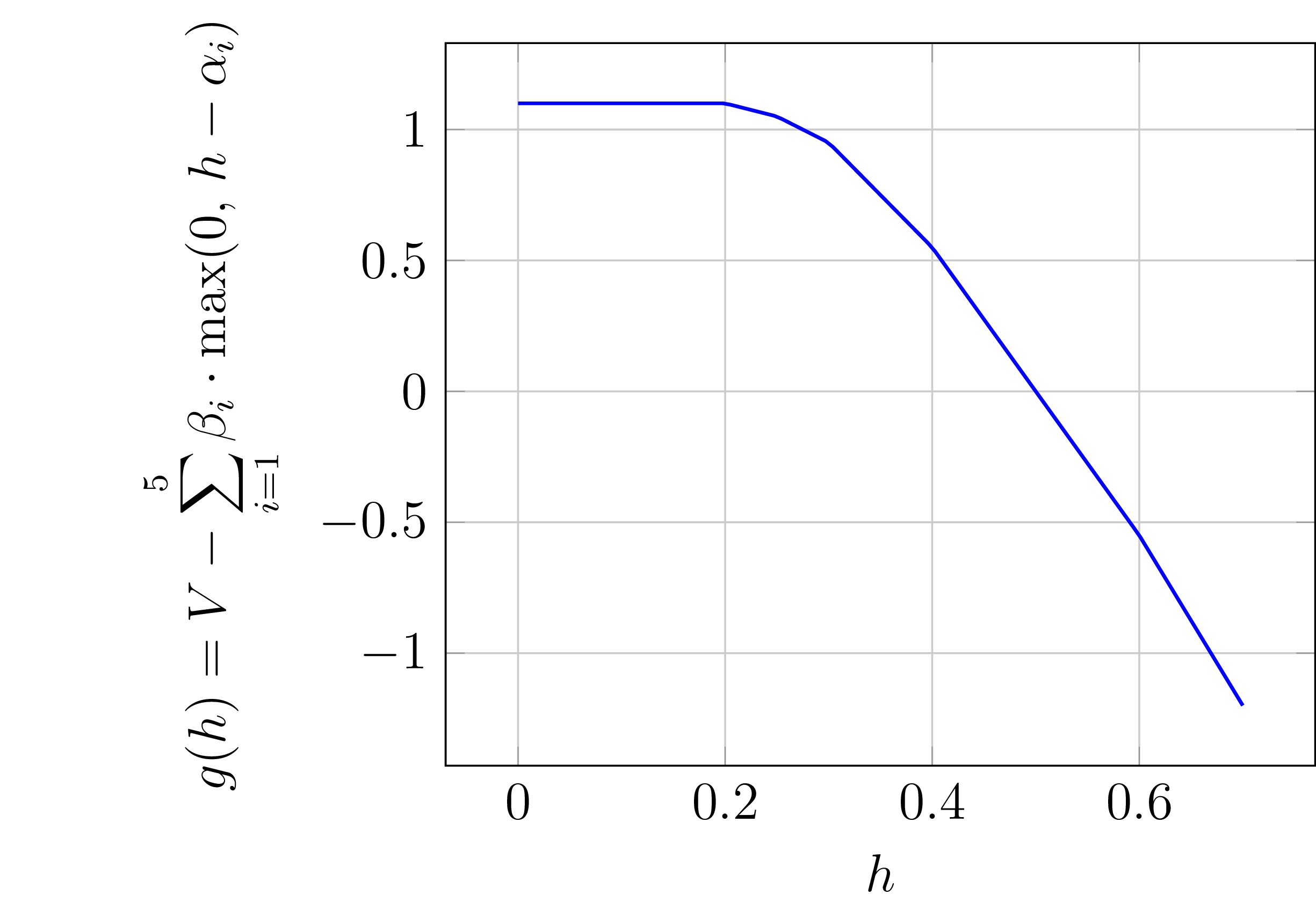
Obrázek č. 6: Obrázek funkce $g$ odpovídající situaci uvedené v obrázku 5.
Rychlá reciproká druhá odmocnina (*Fast inverse square root*)
Newtonova metoda je využita v implementaci funkce $f(x) = \frac{1}{\sqrt{x}}$ ve známe počítačové hře Quake III Arena. Tuto funkci je třeba opakovaně vyhodnocovat při tzv. normalizaci vektoru (podělení vektoru jeho délkou), což je operace prováděná v počítačové grafice velmi často. Newtonova metoda s dobrou první aproximací konverguje velmi rychle a proto se na tento úkol díky této své efektivitě hodí.
Příslušná cenzurovaná část kódu vypadá následovně:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1,5F;
x2 = number * 0,5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the ****?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
První část kódu (až před řádek s komentářem // 1st iteration) spočívá v nalezení první aproximace pro Newtonovu metodu.
Tuto část nebudeme podrobněji rozebírat, zájemce odkazujeme na již dříve zmíněnou stránku.
Poznamenejme, že se využívá znalosti tvaru strojového čísla a uvedený kód je optimalizován pro 32 bitový datový typ (odtud plyne i hodnota oné magické konstanty).
Těsně před koncem těla funkce se provede jeden krok Newtonovy metody (druhý krok je zakomentovaný, protože přesnost získaná v jednom kroku z vhodné počáteční aproximace je prakticky dostatečná).
Skutečně, rovnice \[ f(c) = \frac{1}{\sqrt{c}} = x \] pro zadané $c>0$ a neznámé $x>0$ je ekvivalentní rovnici \begin{equation}\label{eq-fisr} g(x) = c - \frac{1}{x^2} = 0. \end{equation} Derivací funkce $g$ je \[ g'(x) = \frac{2}{x^3} \] a rekurentní vzorec pro Newtonovu metodu odpovídající úloze \eqref{eq-fisr} proto je \[ x_{n+1} = x_n - \frac{g(x_n)}{g'(x_n)} = x_n - \frac{c - \frac{1}{x_n^2}}{\frac{2}{x_n^3}} = \frac{3}{2} x_n - \frac{c x_n^3}{2}, \] což přesně odpovídá zmíněné části kódu (kde si je jen potřeba dát pozor na použité škálování).
Porovnání metod
Porovnejme uvedené metody na několika jednoduchých konkrétních příkladech.
Hledání druhé odmocniny ze dvou
Jako testovací jednoduchý problém si zvolíme hledání druhé odmocniny ze dvou, tj. numerické hodnoty $\sqrt{2}$. Toto číslo je kladným řešením rovnice \[ f(x) := x^2 - 2 = 0. \] Postupně použijeme počáteční nastavení:
- Bisekce: počáteční interval $\langle 1,2 \rangle$,
- *Regula falsi*: počáteční interval $\langle 1,2 \rangle$,
- Newtonova metoda: první aproximace $1$,
- Metoda sečny: první dvě aproximace $1$ a $2$.
Výpočet ve všech případech ukončíme pokud absolutní hodnota poslední aproximace je menší než $\varepsilon = 1{,}4901161193847656 \cdot 10^{-8}$. Ve všech čtyřech případech použijeme aritmetiku 64 bitových čísel s pohyblivou desetinnou čárkou (tj. tzv. *double*).
Shrnutí výsledků je následující (správné cifry jsou označeny pro přehlednost tučně):
- Bisekce: 1,4142135605216026 (27 iterací)
- Regula falsi*: **1,41421356*05326258 (11 iterací)
- Newtonova metoda: 1,4142135623746899 (5 iterací)
- Metoda sečny: 1,4142135626888697 (5 iterací)
- Známá hodnota s přesností na 17 cifer: 1,4142135623730950
Pro zájemce uvádíme i vyčerpávající tabulku s jednotlivými kroky algoritmů. Nejprve pro metodu bisekce.
| # | $a$ | $b$ | $c$ | $|f(c)|$ |
|---|---|---|---|---|
| 1 | 1,0 | 2,0 | 1,5 | 0,25 |
| 2 | 1,0 | 1,5 | 1,25 | 0,4375 |
| 3 | 1,25 | 1,5 | 1,375 | 0,109375 |
| 4 | 1,375 | 1,5 | 1,4375 | 0,06640625 |
| 5 | 1,375 | 1,4375 | 1,40625 | 0,0224609375 |
| 6 | 1,40625 | 1,4375 | 1,421875 | 0,021728515625 |
| 7 | 1,40625 | 1,421875 | 1,4140625 | 0,00042724609375 |
| 8 | 1,4140625 | 1,421875 | 1,41796875 | 0,0106353759765625 |
| 9 | 1,4140625 | 1,41796875 | 1,416015625 | 0,005100250244140625 |
| 10 | 1,4140625 | 1,416015625 | 1,4150390625 | 0,0023355484008789062 |
| 11 | 1,4140625 | 1,4150390625 | 1,41455078125 | 0,0009539127349853516 |
| 12 | 1,4140625 | 1,41455078125 | 1,414306640625 | 0,0002632737159729004 |
| 13 | 1,4140625 | 1,414306640625 | 1,4141845703125 | 8,200109004974365e-5 |
| 14 | 1,4141845703125 | 1,414306640625 | 1,41424560546875 | 9,063258767127991e-5 |
| 15 | 1,4141845703125 | 1,41424560546875 | 1,414215087890625 | 4,314817488193512e-6 |
| 16 | 1,4141845703125 | 1,414215087890625 | 1,4141998291015625 | 3,8843369111418724e-5 |
| 17 | 1,4141998291015625 | 1,414215087890625 | 1,4142074584960938 | 1,726433401927352e-5 |
| 18 | 1,4142074584960938 | 1,414215087890625 | 1,4142112731933594 | 6,474772817455232e-6 |
| 19 | 1,4142112731933594 | 1,414215087890625 | 1,4142131805419922 | 1,0799813026096672e-6 |
| 20 | 1,4142131805419922 | 1,414215087890625 | 1,4142141342163086 | 1,6174171832972206e-6 |
| 21 | 1,4142131805419922 | 1,4142141342163086 | 1,4142136573791504 | 2,687177129701013e-7 |
| 22 | 1,4142131805419922 | 1,4142136573791504 | 1,4142134189605713 | 4,056318516632018e-7 |
| 23 | 1,4142134189605713 | 1,4142136573791504 | 1,4142135381698608 | 6,845708355740499e-8 |
| 24 | 1,4142135381698608 | 1,4142136573791504 | 1,4142135977745056 | 1,0013031115363447e-7 |
| 25 | 1,4142135381698608 | 1,4142135977745056 | 1,4142135679721832 | 1,583661290993632e-8 |
| 26 | 1,4142135381698608 | 1,4142135679721832 | 1,414213553071022 | 2,6310235545778937e-8 |
| 27 | 1,414213553071022 | 1,4142135679721832 | 1,4142135605216026 | 5,236811428943611e-9 |
Nyní pro metodu regula falsi.
| # | $a$ | $b$ | $c$ | $|f(c)|$ |
|---|---|---|---|---|
| 1 | 1,0 | 2,0 | 1,3333333333333333 | 0,22222222222222232 |
| 2 | 1,3333333333333333 | 2,0 | 1,4 | 0,04000000000000026 |
| 3 | 1,4 | 2,0 | 1,411764705882353 | 0,006920415224913157 |
| 4 | 1,411764705882353 | 2,0 | 1,4137931034482758 | 0,0011890606420930094 |
| 5 | 1,4137931034482758 | 2,0 | 1,414141414141414 | 0,00020406081012214194 |
| 6 | 1,414141414141414 | 2,0 | 1,4142011834319526 | 3,501277966488914e-5 |
| 7 | 1,4142011834319526 | 2,0 | 1,41421143847487 | 6,007286838860537e-6 |
| 8 | 1,41421143847487 | 2,0 | 1,4142131979695434 | 1,030688757230891e-6 |
| 9 | 1,4142131979695434 | 2,0 | 1,4142134998513232 | 1,7683827158165855e-7 |
| 10 | 1,4142134998513232 | 2,0 | 1,4142135516460548 | 3,034065154672305e-8 |
| 11 | 1,4142135516460548 | 2,0 | 1,4142135605326258 | 5,2056330357430625e-9 |
Nyní, podstatně rychlejší, Newtonova metoda.
| # | $a$ | $|f(a)|$ |
|---|---|---|
| 1 | 1,0 | 1,0 |
| 2 | 1,5 | 0,25 |
| 3 | 1,4166666666666667 | 0,006944444444444642 |
| 4 | 1,4142156862745099 | 6,007304882871267e-6 |
| 5 | 1,4142135623746899 | 4,510614104447086e-12 |
A konečně metoda sečny.
| # | $a$ | $b$ | $c$ | $|f(c)|$ |
|---|---|---|---|---|
| 1 | 1,0 | 2,0 | 1,3333333333333335 | 0,22222222222222188 |
| 2 | 1,3333333333333335 | 1,0 | 1,4285714285714286 | 0,04081632653061229 |
| 3 | 1,4285714285714286 | 1,3333333333333335 | 1,4137931034482758 | 0,0011890606420930094 |
| 4 | 1,4137931034482758 | 1,4285714285714286 | 1,41421143847487 | 6,007286838860537e-6 |
| 5 | 1,41421143847487 | 1,4137931034482758 | 1,4142135626888697 | 8,931455575122982e-10 |
Z výpočtů je vidět, že bisekce a regula falsi konvergují nejpomaleji. Naopak Newtonova metoda a metoda sečny dosáhnou řeší v požadované přesnosti v podstatně menším počtu iterací.
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).

