Základní potíže při práci s čísly s plovoucí čárkou
Obvyklou reprezentací reálných číslech v počítači je formát s plovoucí čárkou s omezenou pamětí pro cifry a exponent čísla. Na příkladu si uvedeme, jak jednoduše mohou vzniknout chyby v takovém systému a jak lze takové chyby naivně odhadnout.
$\DeclareMathOperator{\fl}{fl} \newcommand\Fl[1]{\fl \left ( #1 \right)}$
Kolik je třeba podložek?
Kapitán Raketka dohlíží na stavbu své nové vesmírné lodi. Stavba se blíží ke konci a čelí následujícímu problému. Dodavatel, Nadvesmírná kovová korporace, spletl objednávku a dodal jednu miliardu špatných podložek pod šrouby. Potíž je v tom, že podložky mají příliš velkou hmotnost. Maximální přípustná hmotnost všech podložek je $L = 1{,}25 \cdot 10^{6}$ kg. Podložky jsou kulaté o vnějším poloměru $R = 0{,}04$ mm.
Kapitán Raketka požádá svého inženýra Trumfa, aby podložky opravil. Tedy aby jim snížil hmotnost tím, že zvětší jejich vnitřní poloměr. Hledanou novou hodnotu vnitřního poloměru budeme značit $r$. Zároveň ho žádá, aby z důvodu bezpečnosti jejich vnitřní poloměr $r$ zvětšil co nejméně. Situace je zobrazena na obrázku č. 1.
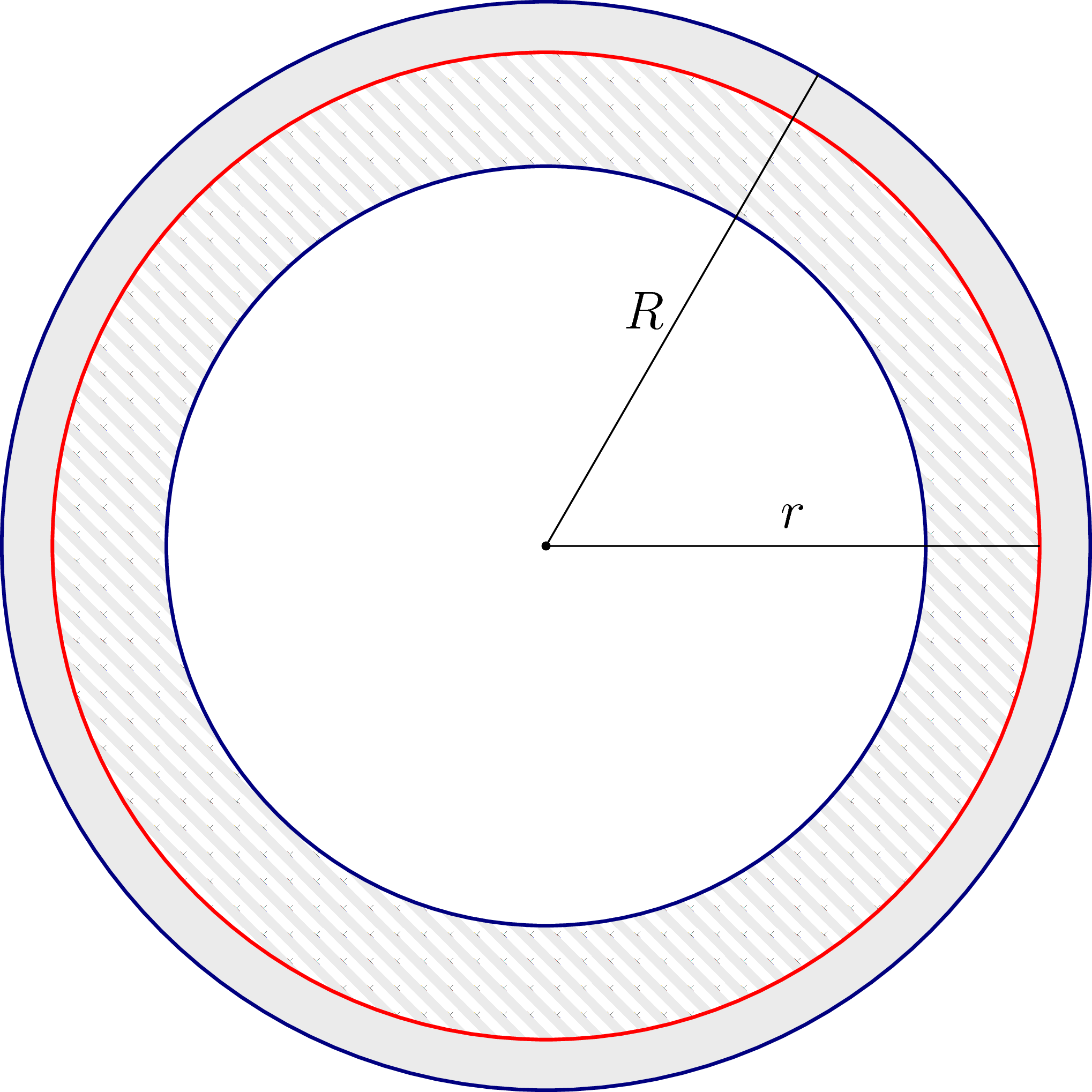
Obrázek č. 1: Kulatá podložka pod šroub. Vnější poloměr je $R$. Inženýr Trumf má nalézt nový vnitřní poloměr $r$ a vyříznutím šrafované části snížit hmotnost podložek.
Kapitán Raketka je věhlasný racionálně uvažující hrdina a potřebuje, aby mu inženýr Trumf dodal nějakou racionální hodnotu. Jeho vybavení si dokonce poradí s jakoukoliv racionální hodnotou, tedy inženýr Trumf není v tomto směru omezen a má husté pole působnosti.
Na Zemi se na druhý pokus podařilo ustanovit hodnotu konstanty $\pi$ na $3{,}14$. Politická obratnost Kapitána Raketky je navíc taková, že v jeho blízkosti je tato hodnota rovna $1$. To inženýru Trumfovi jistě pomůže!
Řešení
Inženýr Trumf si vezme papír a tužku. V tabulkách si vyhledá plošnou hustotu podložek a zjistí, že je to $10{,}1$ kg/mm2. Musí tedy platit \[ (1 \cdot R^2 - 1 \cdot r^2) \cdot 10^9 \cdot 10{,}1 < L, \] kde $R$ je vnější poloměr podložky, $r$ je hledaný vnitřní poloměr podložky a $L$ je celkový limit na hmotnost všech podložek. Označme $Q = 10^9 \cdot 10{,}1$. Dostaneme \[ r \geq \sqrt{R^2 - \frac{L}{Q}}. \] Protože má najít co nejmenší hodnotu $r$, bude řešit rovnost \begin{equation} \label{eq:rovnost} r = \sqrt{R^2 - \frac{L}{Q}}. \end{equation} Do svého počítacího stroje zadá údaje a ten mu vrátí \[ \sqrt{R^2 - \frac{L}{Q}} = 0{,}038421836. \] Inženýr Trumf nechce nechat nic náhodě a proto raději vezme hodnotu $r$ o něco vyšší. Přesněji zvýší o 1 poslední cifru, tedy finálně nastaví \[ r = 0{,}038421837. \] Provede kontrolní výpočet \[ (R^2 - r^2) \cdot Q \] a vyjde mu přesně $L = 1{,}25 \cdot 10^{6}$. Je tedy v limitu a spokojeně běží s výsledkem za kapitánem Raketkou.
Kapitán Raketka nechá podložky upravit podle spočtené hodnoty $r$. Jelikož také nechce nechat nic náhodě, na super přesné vesmírné váze nechá zvážit svou budoucí novou loď před a po namontování podložek. Z hrůzou dojde k závěru, že limit na celkovou hmotnost podložek byl překročen o více než $1{,}5$ kg! To znamená, že s rozjezdem do kopce nelze počítat a stoupne mu průměrná spotřeba!
Co udělal inženýr Trumf za chybu?
Kde byly chyby
První chyba, kterou inženýr Trumf udělal, bylo nepoužití selského rozumu. Podařilo se mu totiž najít dvě hodnoty $r$, přesněji $0{,}038421836$ a $0{,}038421837$, které řeší jeho rovnici \[ (1 \cdot R^2 - 1 \cdot r^2) \cdot 10^9 \cdot 10{,}1 = L. \] Jedná se sice o kvadratickou rovnici, kde lze čekat 0 až 2 řešení, ale již od pohledu je jasné, že máme-li řešení $r$, pak druhé řešení je právě $-r$.
Byla tedy chyba ve vzorci $\eqref{eq:rovnost}$? Vzorec je odvozený správně. Chyba samozřejmě byla v důvěře v počítací stroj, který inženýr Trumf použil. Vždyť právě ten mu v podstatě řekl, že obě hodnoty rovnost \eqref{eq:rovnost} splňují, a to nemůže být pravda. Kladné řešení je právě jedno a je to \[ r = \sqrt{0{,}04^2 - \frac{1{,}25}{10{,}1} 10^{-3}} = \frac{1}{100}\sqrt{\frac{1491}{101}}. \] Trumfův problém je tedy práce s přibližnými hodnotami. Dále se podíváme, co přesně se v Trumfově počítacím stroji událo.
Reprezentace hodnot v počítači
Jako všechny pozemské stroje, tak i ten Trumfův má omezenou paměť a na uložení jednoho čísla si vždy nechá přesně 32 bitů. Obecný tvar ukládaného čísla je následující: \[ \text{znaménko} \cdot \text{signifikand} \cdot \text{báze}^\text{exponent}. \] Báze je určená předem a je rovna 2, abychom mohli výhodné použít dvou hodnot jednoho bitu, $0$ a $1$. Rezervovaných 32 bitů tedy musí obsahovat informace o znaménku, signifikandu a exponentu. Ukládáme-li číslo $x$, tak jeho 32 bitů je rozděleno následujícím způsobem. Jeden bit, označíme jej $s$, určuje, zda je číslo kladné nebo záporné. Celkem 23 bitů slouží pro binární reprezentaci signifikandu, přesněji její větší části. Označíme tyto bity $s_1,s_2,\ldots,s_{23}$. Nakonec 8 bitů je určeno k uložení informace o exponentu, ty označíme $e_1,\ldots,e_8$. Hodnotu čísla $x$ získáme ze vzorce \begin{equation} \label{eq:svz} x = \underbrace{(-1)^s }_{\text{znaménko}} \cdot \underbrace{\left( 1.s_1s_2\ldots s_{23}\right)_2 }_{\text{signifikand}} \cdot 2^{\overbrace{\left( e_1e_2\ldots e_8\right)_2 - 127}^{\text{exponent}}}. \end{equation} Je třeba si všimnout dvou věcí. V signifikandu je napevno první cifra před binární čárkou nastavena na $1$, čímž se ušetří trochu paměti. Této jedničce se často říká skrytá jednička nebo skrytý/implicitní bit. V exponentu figuruje číslo $127$, což je tzv. vychýlení/posunutí (bias), které nám umožňuje získat i záporné exponenty.
Tomuto formátu se říká jednoduchá přesnost (single precision). Je dán standardem IEEE 754 [3], který navíc diktuje, že krajní hodnoty exponentu jsou rezervované pro jiné informace. Konkrétně pokud $e = (e_1e_2 \ldots e_8)_2 = 0$, pak daných 32 bitů reprezentuje subnormální číslo a nepoužívá se obecný vzorec se skrytou jedničkou \eqref{eq:svz}. Pokud je $e$ naopak maximální, tedy $e = 255$, pak je hodnota interpretována nějakým vymezeným specifickým významem. Mezi tyto speciální hodnoty patří například plus a minus nekonečno. Pro všechny ostatní hodnoty $e$ platí \eqref{eq:svz} a říkáme, že číslo $x$ je normalizované. Hodnoty exponentu se tedy pohybují od $1-127 = -126$ až do $254-127 = 127$.
Jelikož v hlavním záběru tohoto formátu jsou normalizovaná čísla, nadále se budeme soustředit pouze na ně. Označme množinu všech normalizovaných čísel $x$ symbolem $\mathcal{M}$. Platí tedy \[ \begin{split} \mathcal{M} = \Big \{ & (-1)^s \cdot \left( 1.s_1s_2\ldots s_{23}\right)_2 \cdot 2^{ \left( e_1e_2\ldots e_8\right)_2 - 127 } \colon \\ & s \in \{0,1\}, 0 < e < 256, 0 \leq \left(s_1s_2\ldots s_{23}\right)_2 \leq 2^23-1 \Big \}. \end{split} \]
Abychom naznačili, jak množina $\mathcal{M}$ vypadá, tak na obrázku č. 2 je vykreslený počet jejích prvků na intervalu pevné délky $\frac{1}{10}$.
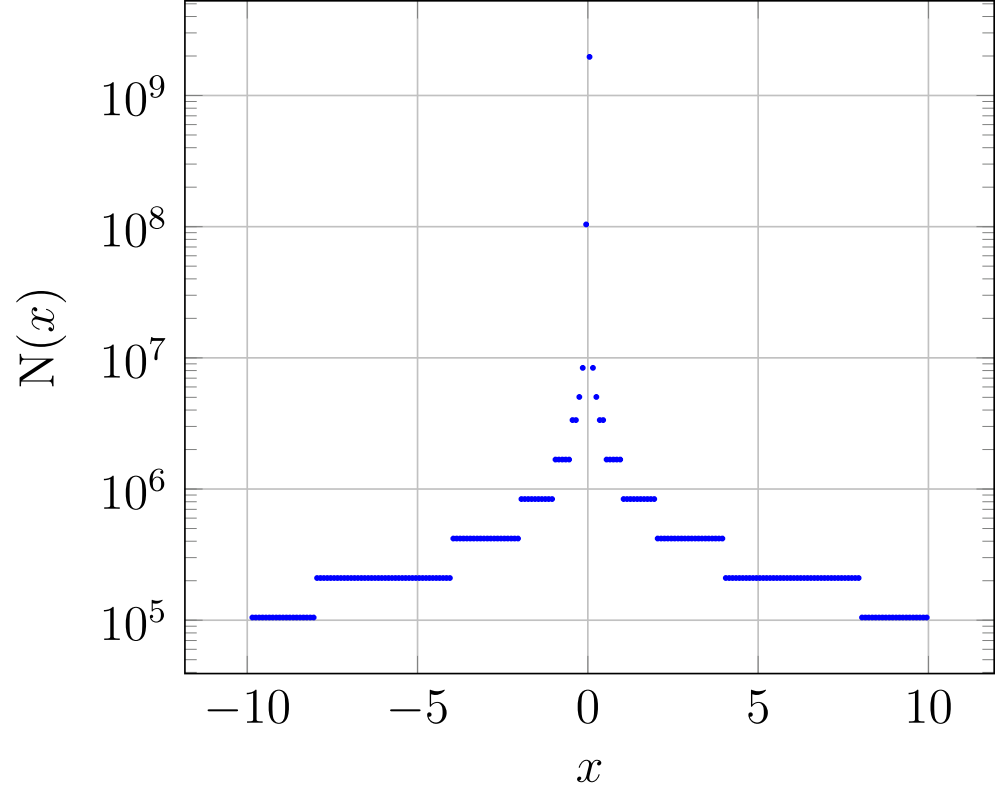
Obrázek č. 2: Hodnotou $N(x)$ značíme počet prvků množiny $\mathcal{M}$ v intervalu o délce $\frac{1}{10}$ rovnoměrně kolem hodnoty $x$. Tato hodnota nám ukazuje, jak jemně či hrubě jednoduchá přesnost pokrývá interval $(-10,10)$. Za povšimnutí stojí, že svislá osa má logaritmické měřítko.
Máme-li nějaké reálné číslo $x$ a chceme s ním v tomto formátu pracovat, tak prvním krokem je najít jeho reprezentaci ve zvoleném formátu. Tedy přesněji najít prvek množiny $\mathcal{M}$, který bude dostatečně dobře reprezentovat hodnotu $x$. Pokud $x \in \mathcal{M}$, tak je řešení jasné. Pokud tomu tak není, taktika bude najít co nejbližšího souseda z $\mathcal{M}$, pokud ovšem nejsme od množiny moc daleko. Připomeňme, že jsme se kvůli zjednodušení vysvětlování omezili pouze na normalizovaná čísla a že se tím dopouštíme drobné nepřesnosti.
Prvním krokem je najít binární reprezentaci čísla $x$, nejlépe takto: \begin{equation} \label{eq:xbin} x = \pm \left(1.x_1x_2x_3 \ldots \right)_2 \cdot 2^q. \end{equation} Uvažujeme, že posloupnost $\left ( x_i \right)_{i=1}^{+\infty}$ má nekonečně mnoho členu; konečné rozvoje doplníme samými nulami na konci. Dále potřebujeme číslo $x$ zaokrouhlit tak, abychom dostali tvar \[ x \approx \widetilde{x} = \pm \left(1.\widetilde{x_1}\widetilde{x_2}\widetilde{x_3} \ldots \widetilde{x_{23}} \right)_2 \cdot 2^{\widetilde{q}}. \] Tedy zaokrouhlujeme na 23. pozici za binární tečkou v \eqref{eq:xbin}. Zaokrouhlovat budeme pomocí pevně zvolené strategie. Tou výchozí je zaokrouhlování k nejbližšímu sousedovi. Číslo, které má dva nejbližší sousedy, se zaokrouhlí podle pravidla „shody na sudé“ (ties to even). Důvodem této volby se zabývat nebudeme, odkážeme se na [1] a [2]. V binární reprezentaci sudým číslem rozumíme to, jehož rozvoj končí na $0$.
Ukažme si toto pravidlo na příkladu. Pro jednoduchost budeme zaokrouhlovat na 3. pozici za binární tečkou. Mějme číslo \[ 0{.}011101, \] které leží mezi $0{.}011$ a $0{.}100$. Jelikož na 4. místě je $1$, a za touto pozicí je ještě nějaká nenulová cifra, tak budeme zaokrouhlovat nahoru, tedy na číslo $0{.}100$. Pokud bychom měli číslo \[ 0{.}011001, \] pak fakt, že na 4. pozici je $0$, nutí zaokrouhlovat dolů na $0{.}011$. Posledním případem je číslo \[ 0{.}0111, \] které má na 4. pozici $1$ a za ním už jen samé nuly. Toto číslo je stejně daleko od čísel $0{.}011$ a $0{.}100$ a na řadu přišlo pravidlo „shody na sudé“. Sudé je $0{.}100$ a to je tedy to číslo, na které zaokrouhlíme. Ještě detailnější rozebrání tohoto postupu lze nalézt v tomto blogu.
Uvedený příklad postihuje všechna pravidla, která ke strategii zaokrouhlování k nejbližším sousedům musíme znát. Dalšími 3 volbami jsou zaokrouhlování k $0$, k $+\infty$ a k $-\infty$. Zvláště zaokrouhlování k $0$ je velice jednoduché, neboť bez ohledu na znaménko stačí zapomenout vše na pozici 24 a výše.
Zaokrouhlením jsme tedy dospěli k číslu $\widetilde{x}$. Pokud je exponent v reprezentovatelném rozsahu, tedy pokud $-126 \geq \widetilde{q} \geq 127$, pak máme našeho vítěze z množiny $\mathcal{M}$. Pokud je exponent příliš malý, hovoříme od podtečení (underflow), pokud je moc velký pak o přetečení (overflow). K signalizaci těchto problémů slouží výše zmíněné speciální hodnoty. Celkem se nám podařilo definovat zobrazení $\fl: \mathbb{R} \to \mathcal{M} \cup \{ ? \}$ takto \[ \Fl{x} = \begin{cases} \widetilde{x} & \text{ pokud } \widetilde{x} \in \mathcal{M}, \\ ? & \text{ jinak.}\end{cases} \] Symbolem $?$ myslíme pro zjednodušení jakýkoliv výjimečný stav.
Měření chyby reprezentace
Dále budeme již uvažovat jen výchozí volbu zaokrouhlování, tedy k nejbližšímu sousedovi. Chybou reprezentace myslíme číslo $| x - \Fl{x} |$. Zachováme značení z předchozí části. Potom můžeme chybu jednoduše odhadnout \[ | x - \Fl{x} | \leq 2^{q-24}. \] Pravá strana odhadu závisí na $x$, proto se místo této absolutní chyby volí chyba relativní, kterou stejným způsobem rovnou odhadneme \[ \frac{| x - \Fl{x} |}{| x |} \leq \frac{2^{q-24}}{\left(1.x_1x_2x_3 \ldots \right)_2 \cdot 2^q} \leq 2^{-24}. \] Hodnotě na pravé straně takto odhadující relativní chybu říká zaokrouhlovací jednotka (unit roundoff error) nebo také *strojové epsilon*. (Je třeba dát pozor, definice se někdy liší a navíc jsou závislé na strategii zaokrouhlování.)
Vraťme se nyní zpět i inženýru Trumfovi a odhadněme jeho chybu.
Chyba v Trumfově výpočtu
Abychom mohli zcela rozumět tomu, kde se chyby ve výpočtu podle \eqref{eq:rovnost} vzaly, museli bychom se věnovat i početním operacím, které Trumf použil. Zmíněný standard IEEE 754 specifikuje i tyto operace. My se nyní tomuto věnovat nebudeme, pokračování této tématiky lze nalézt v příspěvku, který se zabývá sčítáním na počítači. Vhodným výchozím čtením je [2].
Jedinou informací o operacích bude to, že v principu fungují tak, že jejich výsledek je opět reprezentován v množině $\mathcal{M}$ stejným způsobem. Tedy například pro $x,y \in \mathcal{M}$ si lze jejich součet představit jako \[ x \oplus y = \Fl{x+y}, \] kde symbolem $\oplus$ míníme operaci sčítání v jednoduché přesnosti.
Pojďme si nyní odhadnout, kolika desítkovým cifrám výsledku můžeme bezmezně věřit, víme-li, že relativní chyba je omezená hodnotou \[ 2^{-24} \approx 5{,}96 \cdot 10^{-8}. \] Tedy chyby zaokrouhlování jsou na 8. cifře desítkové reprezentace. (Při zobrazování desítkových reprezentací čísel v jednoduché přednosti proto nemá cenu obecně zobrazovat více než $7$ cifer.)
Inženýr Trumf vrací výsledek $r = 0{,}038421837$, a to zvýšení 8. cifry o 1 oproti získanému výsledku. To je ovšem přesně pozice, kde lze řádově čekat chybu. Proto mu také vyšla kladně „kontrola“ správnosti výsledku: platí totiž $\Fl{0{,}038421836} = \Fl{0{,}038421837}$.
Co se děje dále při výpočtu $(R^2-r^2)\cdot Q$? Chyba v čísle $r$ je řádu $10^{-10}$. Umocněním $r^2$ se neposune, odečtením $R^2$ se také (obecně) nic nestane. Přenásobením $Q \approx 10^{10}$ se nám chyba dostane do řádů jednotek, což je ten rozdíl $1{,}5$ kg, který nám vyšel. (Tento rozdíl jsme zjistili pomocí *dvojité přesnosti*, která „vidí správně“ 15 desítkových míst.)
Je důležité poznamenat, že náš pohled na chybu ve výpočtu je do jisté míry naivní, nicméně v našem případě postačující k tomu, abychom určili, na jakém řádu lze chybu čekat. Řád, kde lze chybu čekat, a tedy i spolehlivost výsledku, samozřejmě také ovlivňuje počet operací, a tedy reprezentací, které jsme provedli. Výsledná chyba navíc závisí i na vlastních hodnotách, které při špatném nastavení mohou ještě zhoršit (nebo paradoxně i zlepšit) kvalitu výsledku. To, že na nějakém řádu lze chybu čekat neznamená, že tam bude. Již zmíněný příspěvek, který se zabývá sčítáním na počítači, se věnuje některým z těchto jevů.
Na závěr uveďme odkaz na server root.cz, kde se lze srozumitelně (česky) dočíst o reprezentaci čísel s plovoucí čárkou a provádění aritmetických operací.
Použitá literatura
- J. F. Reiser, D. E. Knuth. Evading the drift in floating-point addition, Information Processing Letters. 3: 84-87. DOI: 10.1016/0020-0190(75)90022-8
- D. Goldberg. What Every Computer Scientist Should Know About Floating-Point Arithmetic, Computing Surveys, March, 1991, Association for Computing Machinery, Inc. editovaná online verze
- IEEE STANDARD 754-2008 - IEEE Standard for Floating-Point Arithmetic, IEEE, 2008, online
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).

