Nástrahy sčítání pomocí počítače
V počítačích běžně používaná reprezentace čísel s plovoucí čárkou je spojená s chybami, které vznikají při výpočtech. Podíváme se na chyby, které se mohou vyskytnou při počítání sum. Naší motivací pro výpočet takové sumy je získání přibližné funkční hodnoty přirozeného logaritmu ze dvou.
$\DeclareMathOperator{\N}{\mathcal{N}} \newcommand\Num[1]{\N \left ( #1 \right)}$
Kolik je $\ln(2)$?
V dnešní době všudypřítomných počítačů a internetu není problém provádět výpočty, které by byly s tužkou a papírem na dlouho. Podíváme se, jak lze spočíst přibližnou hodnotu čísla $\ln(2)$, tedy přirozeného logaritmu ze dvou. Jedná se o tzv. transcendentní číslo: není kořenem žádného polynomu s racionálními koeficienty, který by se pro spočtení hledané přibližné hodnoty dal použít. Použijeme jeden ze základních nástrojů a to Taylorovu větu.
Taylorova věta
Taylorovu větu použijeme k výpočtu přibližné hodnoty $\ln(2)$ následujícím způsobem. Budeme aproximovat funkci $\ln(x)$ pomocí polynomu a odhadneme chybu, kterou jsme udělali. Parametrem této metody je stupeň polynomu $N$. Situace vypadá takto: \[ \ln(x) = P_N(x) + R_N(x), \] kde $P_N(x)$ je polynom stupně $N$ a $R_N(x)$ je chyba, která tímto přiblížením vznikla.
Taylorova věta nám říká, jak výhodně volit polynom $P_N(x)$ a jak lze odhadnout zbytek $R_N(x)$. Obecné tvrzení zní, že pokud má funkce $f$ konečnou $(N+1)$-ní derivaci na nějakém okolí $H_a$ bodu $a$, pak pro polynom \[ P_N(x) = \sum_{k=0}^N \frac{f^{(k)}(a)}{k!}(x-a)^k, \] kterému se říká Taylorův polynom stupně $N$ funkce $f(x)$ v bodě $a$, platí \begin{equation} \label{eq:RNob} R_N(x) = \frac{f^{(N+1)}(\xi)}{(N+1)!}(x-a)^{N+1}, \end{equation} kde $x \in H_a$ a $\xi$ závisí na $x$ i $N$ a leží v intervalu s krajními body $a$ a $x$. Tomuto tvaru chyby $R_N(x)$ se říká *Langrangeův tvar zbytku*.
Pro naše potřeby volíme $f(x) = \ln(x)$ a $a = 1$. Přirozený logaritmus lze na okolí bodu $1$ bezpečně derivovat, dostaneme $f^{(k)}(x) = (-1)^{k-1}\frac{(k-1)!}{x^k}$ pro $k > 0$. Polynom $P_N(x)$ tedy vypadá následujícím způsobem: \[ P_N(x) = 0 + \frac{1}{1} (x-1) - \frac{1}{2} (x-1)^2 + \frac{1}{3} (x-1)^3 + \ldots + \frac{(-1)^{(N+1)}}{N} (x-1)^N. \] Nyní odhadneme velikost chyby $| R_N(x) |$. Chceme spočíst přibližnou hodnotu $\ln(2)$, tedy volíme $x = 2$. Hodnota $\xi$ leží v intervalu $(1,2)$. Můžeme odhadnout $f^{(N+1)}(\xi)$ z \eqref{eq:RNob} takto: \[ | f^{(N+1)}(\xi) | \leq | f^{(N+1)}(1) | = N! \] (Tento odhad funguje dokonce pro všechna $x > 1$.) Dostaneme \begin{equation} \label{eq:RN} | R_N(x) | \leq N! \frac{(x-1)^{N+1}}{(N+1)!} = \frac{(x-1)^{N+1}}{N+1}. \end{equation} Graf funkce $\ln(x)$ a jejího Taylorova polynomu (pro menší hodnotu $N$) je na Obrázku č. 1.
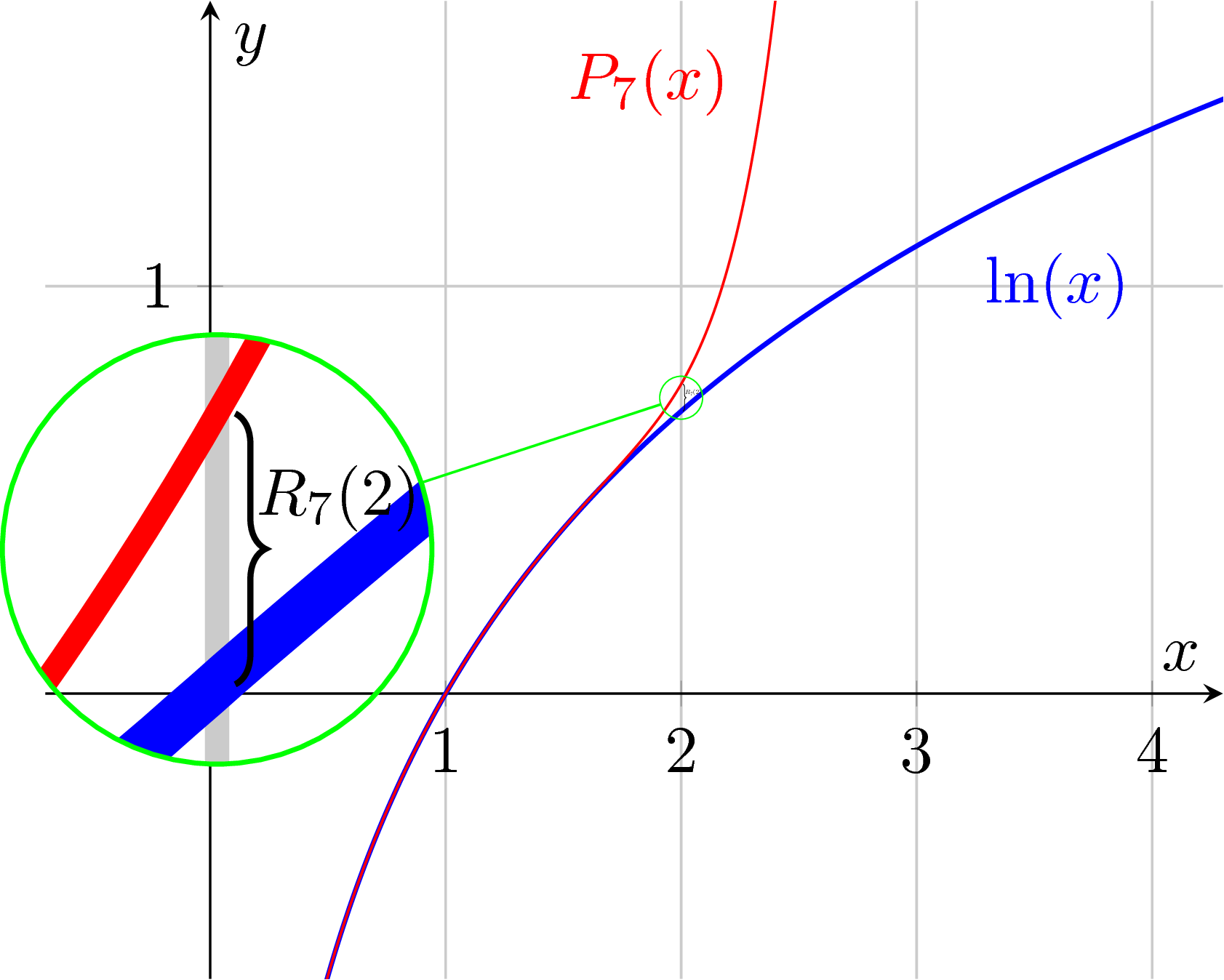
Obrázek č. 1: Použití Taylorova polynomu stupně $7$ v bodě $1$ pro aproximaci funkce $\ln(x)$.
Tedy pro $x=2$ napočítáme odhad hodnoty $\ln(2)$ výpočtem $P_N(2)$ s tím, že odhad chyby je dán hodnotou $\frac{1}{N+1}$. Chceme-li zvýšit přesnost, stačí zvýšit $N$. To je pěkné.
Výpočty
Nebudeme se držet při zdi a rovnou navolíme $N = 10^6$. Pro dnešní počítače není takový výpočet vůbec žádný problém.
Protože budeme chtít nějakým způsobem svůj výpočet ohodnotit, požádáme kouzelného dědečka o skutečnou hodnotu čísla $\ln(2)$. Prvních $7$ správných cifer desetinného rozvoje tohoto čísla je \[ \ln(2) \approx 0{,}6931472. \] Správně napočítaným cifrám se říká platné nebo významné cifry (significant digits). U všech výsledků níže budeme ukazovat právě $7$ cifer (počítáno od té první nenulové).
Počítač nám řekne, že \[ P_{10^6}(2) \approx 0{,}6931483. \] Napočítaná hodnota se liší od skutečné zhruba o $1,1 \cdot 10^6$. To je očekávané, polynom $P_N(x)$ nám umožňuje počítat jen přibližné hodnoty. Koukneme se na připravený vzorec pro odhad chyby: \[ \frac{1}{N+1} = \frac{1}{10^6+1} \approx 9{,}999990 \cdot 10^{-7}. \] To není pěkné. Rozdíl sice není velký, ale stačí na to, aby bylo vidět, že odhad \eqref{eq:RN} neplatí.
Zdá-li se snad někomu taková chyba zanedbatelná, je na čase informovat se o tom, jaké může mít důsledky. Jedna z nejznámějších katastrof, které způsobila numerická chyba, je selhání rakety Patriot.
Zkušeným uživatelům počítačů je jasné, že je čas prozradit detaily našeho výpočtu. Problém není v tom, že by odhad \eqref{eq:RN} neplatil, ten platí. Problém je v tom, že počítač nespočítal přesnou hodnotu $P_{10^6}(2)$, ale pouze nějakou její aproximaci $\Num{P_{10^6}(2)}$, kde značením $\Num{x}$ myslíme nějakou přibližnou hodnotu čísla $x$.
K výpočtům jsme použili reprezentaci čísel s plovoucí čárkou (floating point number), přesněji jsme použili čísla s jednoduchou přesnosti (single precision). Reprezentace je založená na tom, že každé číslo má omezenou paměť, která slouží k jeho uložení. Této reprezentaci se věnujeme v příspěvku, který ilustruje základní úskalí s jejím (bezhlavým) používáním.
Omezení paměti pro jedno číslo, v našem případě 32 bitů, má jeden přímý důsledek, který se týká výše uvedeného výpočtu. Skoro při jakémkoliv výpočtu s tímto datovým typem vznikají chyby. Podívejme se nyní, jak lze takové chyby odhadovat, a tím tedy zpět získat kontrolu nad naším výpočtem.
Jak počítač nakládá s čísly
Základním zdrojem chyb je zaokrouhlování, pomocí kterého hledáme nejbližší hodnotu, která se nám hodí a na kterou nám stačí zvolený datový formát. Pro aritmetické operace lze odhadnout vzniklou chybu následujícím způsobem. Nechť $x$ a $y$ jsou dvě hodnoty, které již máme v počítači reprezentovány v jednoduché přesnosti. Pro operaci $x \odot y$, kde astronomický symbol pro Slunce $\odot$ značí jednu z operací $+,\cdot,/$, platí \begin{equation} \label{eq:operace} \Num{x \odot y} = (x+y)(1+\delta), \quad \text{ kde } | \delta | \leq \mathbf{u}. \end{equation} Hodnotě $\mathbf{u}$ pro takto vyjádřenou relativní chybu výpočtu se říká zaokrouhlovací jednotka (unit roundoff error). Někdy se této mezi také říká strojové epsilon. V našem případě platí $\mathbf{u} = 2^{-24}$. Tato hodnota přesně odpovídá pozici v binárním rozvoji, které se již do naší reprezentace nevejde. Tedy přesně té pozici, na které dochází k zaokrouhlování.
Někdy se k odhadování přesnosti používá i tzv. „ulps“ z anglického unit in the last place, tedy jednotky na posledním místě.
Abychom si trochu zjednodušili úlohu, tak se zaměříme pouze na sčítání v našem výpočtu $\Num{P_N(x)}$. Ostatně ve zmíněném selhání rakety Patriot se problém vyskytl právě v sumě mnoha prvků.
Co se děje při sčítání
Podívejme se nejprve, co se bude dít, když necháme počítač sečíst tři čísla $x$, $y$ a $z$. Nejprve sečte první dvě a dostane podle \eqref{eq:operace} \[ \Num{x+y} = (x+y)(1+\delta_1), \quad \text{ kde } | \delta_1 | \leq \mathbf{u}. \] K takto získanému číslu přičte $z$, a opět aplikací dostaneme. \[ \begin{split} \Num{x+y+z} & = \Num{\Num{x+y}+z} = \Num{(x+y)(1+\delta_1) + z} = \\ & = ((x+y)(1+\delta_1)+z)(1+\delta_2), \end{split} \] kde $| \delta_2 | \leq \mathbf{u}$. Poslední výraz lze drobně přepsat: \begin{equation} \label{eq:xyz} ((x+y)(1+\delta_1)+z)(1+\delta_2) = (x+y+z)(1+\delta_2) + (x+y)(\delta_1 + \delta_1\delta_2). \end{equation} Lze si tedy představit, jak by vypadal takový odhad součtu $4$ a více členů. Uvedeme výsledek tohoto odhadu v čitelnějším tvaru, než jak by dopadl opakovaným používáním \eqref{eq:operace}.
Označme \[ S_N = \sum_{i=0}^{N} x_i, \] kde $x_i$ jsou nějaká čísla v jednoduché přesnosti. (Tiše předpokládáme, že při sčítání nedojde k přetečení či podtečení.) Platí, že \begin{equation} \label{eq:odhad1} | \Num{S_N} - S_N | \leq \frac{N\mathbf{u}}{1-N\mathbf{u}} \sum_{i=0}^{N} | x_i |. \end{equation} Více lze najít v [1].
Odhad, který nám umožnil získat poslední nerovnost, nám zakryl jednu vlastnost chyby: záleží na pořadí sčítání. Toto je patrné z \eqref{eq:xyz}. Také je vidět, že chyba vlastně závisí na $\sum_{i=0}^{N} | x_i |$ a nikoliv $| S_N |$. Tedy případ, kdy platí $\sum_{i=0}^{N} | x_i | \gg | S_N |$, může z hlediska relativní chyby dopadnout mnohem hůře. Přesně to je první zdroj problému ve výpočtu $\Num{P_N(x)}$. Sčítaná řada totiž mění znaménka.
Odčítání dvou podobných hodnot je ostatně dalším obecným zdrojem problémům při práci s čísly s plovoucí čárkou. Ve výsledku odečítání vznikají na konci reprezentace cifry, které jsou z hlediska datového typu platné, ale nejsou to správné cifry: nemají nic společného s výsledkem. Tomuto jevu říká často katastrofické krácení (catastrophic cancellation). Dále se mu již nebudeme věnovat.
Jak lze součet provést jinak
Ve světle obou poznámek k získanému odhadu na chybu při výpočtu $\Num{S_N}$ se můžeme pokusit jednoduše sečíst kladné a záporné členy odděleně. Dostaneme \[ P_{10^6}(2) \approx 0{,}6931477, \] což odpovídá chybě zhruba \[ 5 \cdot 10^{-7}. \] Tedy skutečně došlo ke zlepšení, neboť nyní už jsme pod hranicí odhadu na $R_{10^6}(2)$ a tedy součet byl proveden s menší chybou. Je třeba být na pozoru, protože fakt, že nám vyšel přesnější výsledek, není pravidlem. Tím, že sečteme kladné a záporné členy zvlášť riskujeme to, že efekt katastrofického krácení při sčítání obou sum bude ještě horší, než když se sčítaly samotné členy přímo.
Jinou metodou, která je méně naivní než rozdělení na kladné a záporné členy, je *Kahanův vzorec*. Jeho myšlenkou je provést drobnou opravu po každém přičtení. Účinnost této opravy je založená na předpokladu, že $| S_i | > | x_{i+1} |$. Odhad chyby vzniklé při přičítání $x_{i+1}$ k $S_i$ je dán předpisem $(S_i - \Num{S_i}) + x_{i+1}$. Celkem kód (v jazyku Python) vypadá takto.
s = 0 # výsledná suma
e = 0 # proměnná pro opravu chyby
for i in range(N):
temp = s
y = x[i] + e
s = temp+y
e = (temp-s)+y
Lze dokázat, že tímto algoritmem dosáhneme následujícího odhadu chyby \[ | \Num{S_N} - S_N | \leq \left(2 \mathbf{u} + \mathcal{O}(N\mathbf{u}^2) \right) \sum_{i=0}^{N} | x_i |. \] Pokud $N\mathbf{u} < 1$, je náš odhad v podstatě nezávislý na $N$, což je velký pokrok v porovnání s odhadem \eqref{eq:odhad1}. Ani tento odhad ovšem neznamená, že by algoritmus měl skončit s malou relativní chybou a to především pro případ $\sum_{i=0}^{N} | x_i | \gg | S_N |$.
Vraťme se zpět k výpočtu $P_N(2)$. Vzhledem k tomu, že suma splňuje předpoklad pro dobrou účinnost Kahanova vzorce, lze čekat zlepšení. Skutečně, jeho použitím dostaneme opět \[ P_{10^6}(2) \approx 0{,}6931477, \] což je s touto přesností stejný výsledek jako při odděleném sčítání kladných a záporných členů.
Za zmínku stojí, že autor tohoto algoritmu, William Kahan, je také považován za hlavního autora standardu IEEE 754 z roku 1985 a od té doby se na jeho vývoji stále podílí.
Jiné možnosti
V [1] lze najít další možnosti, jak lze součet mnoha prvků provádět včetně důkazů odhadů napáchaných chyb. Autor [2] na tuto práci navazuje a ještě tak rozšiřuje seznam algoritmů, které lze použít.
Na konec je třeba zmínit možnost využití jiné reprezentace čísel. V první řadě lze uvažovat o přesné reprezentaci. Taková existuje i pro mnoho iracionálních čísel. V druhé řadě se lze obrátit k aritmetikám, které nějakým způsobem hlídají přesnost svých výpočtů. Mezi ně patří používaní tzv. hlídacích bitů nebo intervalových reprezentací. Zkoumání druhého zmíněného lze začít například formátem unum.
Závěrečné poznámky k původní sumě
Poslední poznámkou se vrátíme k našemu odhadu chyby, který je dán hodnotou $\frac{1}{N+1}$. Námi zvolená reprezentace umožňuje důvěryhodně reprezentovat zhruba $7$ desetinných cifer. Pokud by hodnota $N$ byla taková, že by odhad chyby byl za touto hranicí, nemá pak již vůbec smysl takové členy sčítat, protože se teoreticky nelze dostat (v dané přesnosti) blíže k reálné hodnotě a už bychom jen kumulovali chybu. (Samozřejmě bychom mohli dostat i lepší výsledek, ale to by bylo zcela dílem náhody.) Tedy naše volba $N = 10^{6}$ je v kontextu této poznámky ještě rozumná. Pokud si vypíšeme chybu aproximace pro rostoucí $N$, zjistíme, že naše volba byla přeci jen zbytečně velká. Výsledky jsou v následující tabulce.
| $N$ | chyba | $N$ | chyba |
|---|---|---|---|
| $5000$ | $1{,}000185 \cdot 10^{4}$ | $85000$ | $5{,}843160 \cdot 10^{6}$ |
| $10000$ | $4{,}989099 \cdot 10^{5}$ | $90000$ | $5{,}545137 \cdot 10^{6}$ |
| $15000$ | $3{,}320169 \cdot 10^{5}$ | $95000$ | $5{,}247113 \cdot 10^{6}$ |
| $20000$ | $2{,}485704 \cdot 10^{5}$ | $100000$ | $5{,}008695 \cdot 10^{6}$ |
| $25000$ | $1{,}985025 \cdot 10^{5}$ | $150000$ | $3{,}280160 \cdot 10^{6}$ |
| $30000$ | $1{,}651239 \cdot 10^{5}$ | $200000$ | $2{,}445695 \cdot 10^{6}$ |
| $35000$ | $1{,}418781 \cdot 10^{5}$ | $250000$ | $1{,}968858 \cdot 10^{6}$ |
| $40000$ | $1{,}239967 \cdot 10^{5}$ | $300000$ | $1{,}670835 \cdot 10^{6}$ |
| $45000$ | $1{,}102876 \cdot 10^{5}$ | $350000$ | $1{,}313207 \cdot 10^{6}$ |
| $50000$ | $9{,}896276 \cdot 10^{6}$ | $400000$ | $1{,}134393 \cdot 10^{6}$ |
| $55000$ | $9{,}002206 \cdot 10^{6}$ | $500000$ | $1{,}134393 \cdot 10^{6}$ |
| $60000$ | $8{,}286950 \cdot 10^{6}$ | $600000$ | $1{,}134393 \cdot 10^{6}$ |
| $65000$ | $7{,}631299 \cdot 10^{6}$ | $700000$ | $1{,}134393 \cdot 10^{6}$ |
| $70000$ | $7{,}094857 \cdot 10^{6}$ | $800000$ | $1{,}134393 \cdot 10^{6}$ |
| $75000$ | $6{,}618020 \cdot 10^{6}$ | $900000$ | $1{,}134393 \cdot 10^{6}$ |
| $80000$ | $6{,}200788 \cdot 10^{6}$ | $1000000$ | $1{,}134393 \cdot 10^{6}$ |
Lze pozorovat, že pro $N \geq 400000$ se chyba již nemění. Po sobě jdoucí členy na takto vysokých pozicích jsou totiž z hlediska přesnosti již skoro stejné a s celkovým součtem už nic neudělají. Celková pozorovaná chyba se nakumuluje již pro $N = 400000$.
Poslední obecnou poznámkou je, že odhad na chybu $\frac{1}{N+1}$ klesá s rostoucím $N$ velice pomalu. Je nutné učinit závěr, že takovéto použítí Taylorova polynomu pro výpočet přibližné hodnoty $\ln(2)$ je zkrátka nevhodný, a to i když se s chybami při počítání součtu tolika čísel dobře vypořádáme.
Použitá literatura
- Nicholas J. Higham, The Accuracy of Floating Point Summation, SIAM Journal on Scientific Computing, 1993, Vol. 14, No. 4, pp. 783-799, DOI: 10.1137/0914050
- John Michael McNamee, A comparison of methods for accurate summation, ACM SIGSAM Bulletin: Volume 38 Issue 1, March 2004, DOI: 10.1145/980175.980177
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).


Jednoduchý příklad katastrofického sčítání a odčítaní, převzatý z článku citovaného v předchozím blogpostu: číslo $((2 \times 10^{-30} + 10^{30}) - 10^{30}) - 10^{-30}$ je přesně $10^{-30}$, ale ve floating-point aritmetice je výsledkem $-10^{-30}$. Stane se to takto:
K velmi malému číslu jsme přičetli obrovské číslo, které jej zcela "zastínilo", a hned je zase odečetli; výsledkem je čistá nula. Zájemce může projít v bitové reprezentaci všechny zúčastněné operace - klíčové je přičtení čísla
0x7149f2cak číslu0x0e224260.