Kubická interpolace
Při práci s počítačovou grafikou (vizualizace, tvorba grafických uživatelských rozhraní) můžeme narazit na problém jak spojit zadanou množinu bodů křivkou tak, aby tato křivka vypadala hezky, hladce. V následujícím textu si ukážeme jak tento oříšek lze vyřešit pomocí interpolace.
Popis problému
Slovo interpolace pochází s latinských slov inter (mezi) a polire (leštit). Cílem úlohy nesoucí toto označení je sestrojit funkci, jejíž graf prochází předepsanou množinou bodů. Zde se budeme zabývat základní variantou úlohy, kdy všechny body leží v rovině a ve zvoleném pravoúhlém souřadném systému jsou vzestupně seřazeny podle jejich první souřadnice. Takové body lze spojit grafem funkce jedné reálné proměnné. Úlohu ale lze zobecnit i do vyšších dimenzí nebo interpolovat pomocí složitějších křivek, které nutně nemusí být grafy funkcí. Těmito zobecněními se na tomto místě pro jednoduchost zabývat nebudeme.
Začněme nejprve podrobnějším popisem výše zmíněné úlohy. Máme pravoúhlý souřadný systém s osami $x$ a $y$. Dále je zadáno $n \geq 2$ vzájemně různých bodů \[ A_i = (x_i, y_i), \quad i = 1,2,\ldots, n. \] Rovnou předpokládáme uspořádání bodů vzestupně podle jejich $x$-ové souřadnice, tj. předpokládáme platnost nerovností $x_1 < x_2 < \cdots < x_n$. Nepřipouštíme rovnost dvou $x$-ových souřadnic u dvou různých bodů (v tom případě by body nebylo možné spojit grafem funkce). Situaci schematicky znázorňuje následující obrázek.
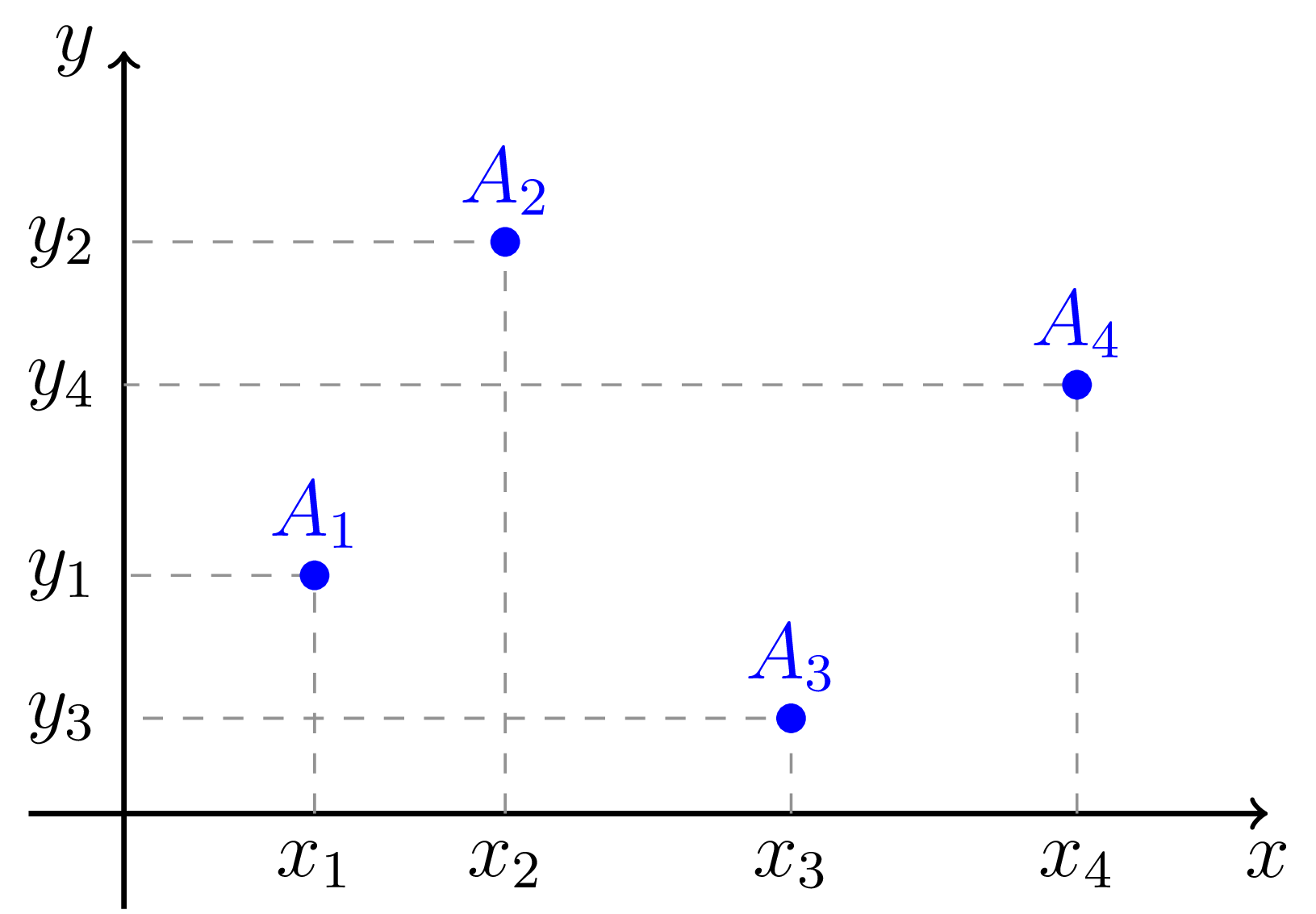
Obrázek č. 1: Příklad množiny čtyř bodů $A_1, A_2, A_3$ a $A_4$ určených k interpolaci.
Cílem našeho snažení je sestrojit funkci $f: \langle x_1, x_n \rangle \to \mathbb{R}$, jejíž graf prochází všemi body $A_i$, $i=1,2,\ldots,n$, tedy funkci splňující \[ f(x_i) = y_i, \quad i=1,2,\ldots, n. \] Takových funkcí je samozřejmě nekonečně mnoho. Úloha proto nemá jednoznačné řešení. Z toho důvodu se omezíme pouze na jistou vybranou třídu funkcí a přidáme na hledanou funkci ještě další podmínky.
Polynomiální interpolace
Pokusme se dva sousední body spojovat (interpolovat) pomocí polynomů stupně nejvýše $m \in \mathbb{N}$. Hledáme proto funkci $f$ po částech polynomiální mající na intervalu $\langle x_i, x_{i+1}\rangle$, $i=1,2,\ldots,n-1$, tvar \[ f_i(x) = \sum_{j=0}^m a_{i,j} x^j, \] kde $x \in \langle x_i, x_{i+1}\rangle$ a $i=1,2,\ldots,n-1$. Každý z polynomů $f_i$, $i=1,2\ldots,n-1$ je zadán $m+1$ konstantami. Abychom tyto polynomy zadali, potřebujeme určit všech $(m+1)\cdot(n-1)$ konstant $a_{i,j}$, $i=1,2,\ldots,n-1$, $j=0,1,\ldots,m$. Příklad po částech polynomiální interpolační funkce je znázorněn na následujícím obrázku 2.
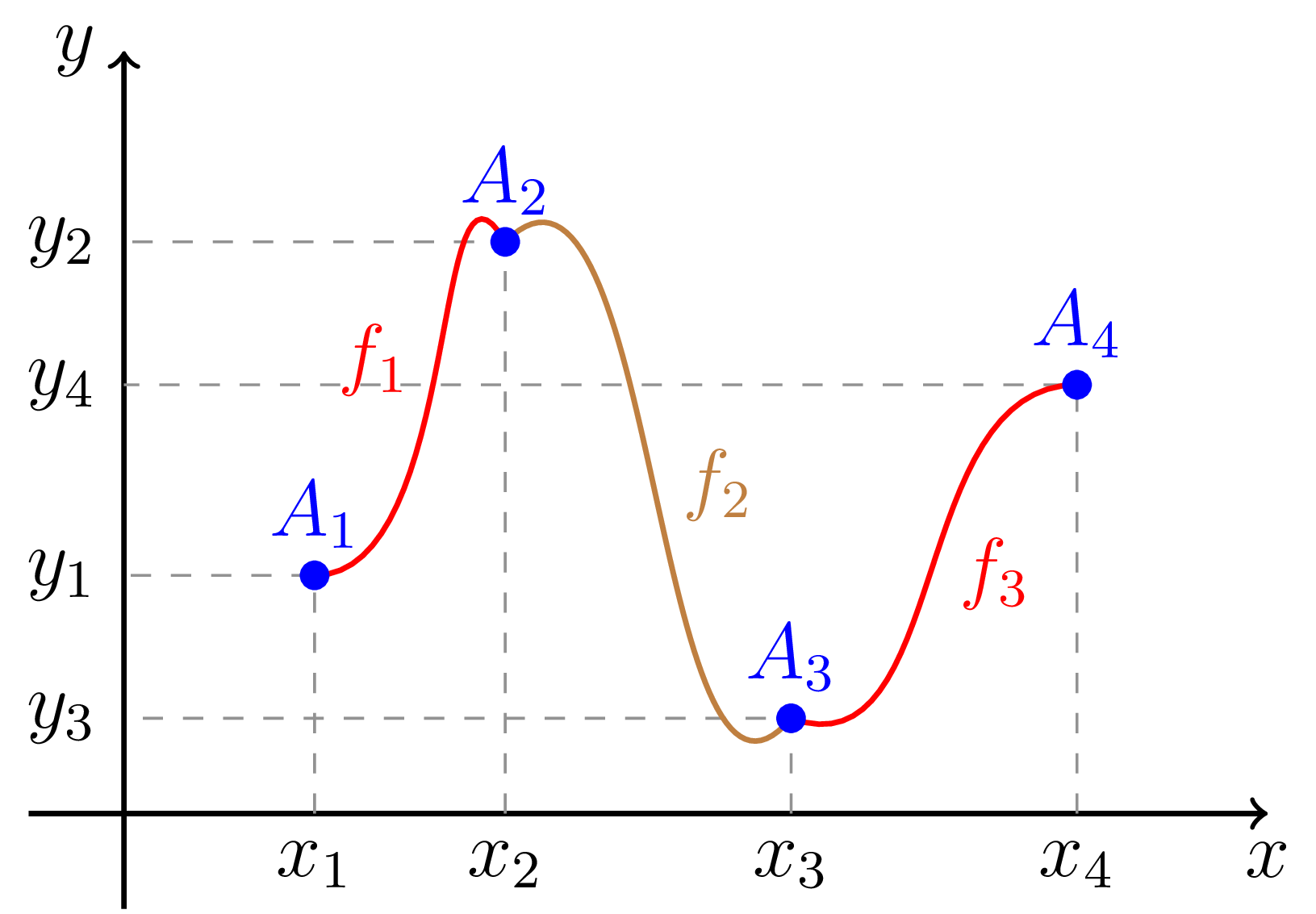
Obrázek č. 2: Příklad po částech polynomiální interpolační funkce $f$.
Po těchto $n-1$ funkcích $f_i$, $i=1,2,\ldots,n-1$, požadujeme, aby vždy na krajích svých definičních oborů procházely předepsaným body. Máme tedy $2(n-1)$ podmínek \[ f_i(x_i) = y_i \quad \text{a} \quad f_i(x_{i+1}) = y_{i+1}, \quad i = 1,2,\ldots,n-1. \] Pokud $m = 1$, pak tyto podmínky jsou dostatečné k určení všech polynomů $f_i$ (dva body v rovině jednoznačně určují přímku, graf polynomu stupně nejvýše $1$).
Pokud je ovšem $m > 1$, pak těchto $2(n-1)$ podmínek je zcela jistě málo k určení $(m+1)\cdot(n-1)$ konstant $a_{i,j}$. Naklademe proto na spoje, či švy, další podmínky zaručující rovnost nejen funkčních hodnot, ale i derivací v těchto bodech. Požadujeme tedy \[ f^{(j)}_{i}(x_{i+1}) = f^{(j)}_{i+1}(x_{i+1}), \quad j=1,2,\ldots,m-1, \ i=1,2,\ldots,n-2. \] To je celkem $(m-1)\cdot(n-2)$ podmínek. Tyto podmínky lze interpretovat jako podmínky na hezkost švů. V napojeních budou mít sousední funkce stejné derivace, spoje tedy nebudou zlomené. Shodnost prvních derivací totiž implikuje shodnost tečen a tedy i směrnic grafů v bodě spojů. Podobně stejnost druhých derivací znamená stejnou vypouklost grafů v bodě spojů. Vyšší derivace již není tak snadné interpretovat, v našem kubickém případě ale ani vyšší než druhé derivace nepotřebujeme.
Požadavek na předepsané funkční hodnoty nám dává $2(n-1)$ podmínek, požadavek na derivace pak $(m-1)\cdot(n-2)$ podmínek. Stále nám \begin{align*} (m+1)\cdot(n-1) - 2(n-1) - (m-1)(n-2) &= (m-1)(n-1) - (m-1)(n-2) = \\ &= m - 1 \end{align*} podmínek zbývá. Bývá zvykem sadu již uvedených podmínek doplnit podmínkami na derivace funkcí na krajích intervalu $\langle x_1, x_n\rangle$, na kterém interpolujeme. Konkrétní volbu si ukážeme níže.
Kubická interpolace (*Splines*)
Velmi častou volbou pro stupeň polynomů při interpolaci je $m=3$ (tzv. kubická interpolace, spline). V tomto případě funkce $f_i$ mají tvar \[ f_i(x) = a_{i,0} + a_{i,1} x + a_{i,2} x^2 + a_{i,3} x^3, \] kde $x\in\langle x_i, x_{i+1}\rangle$, $i = 1,2,\ldots, n-1$. Ve švech se musí rovnat funkční hodnoty a první i druhé derivace spojovaných funkcí. Konečně, na krajích potřebujeme ještě naklást dvě (nyní $m-1 = 2$) podmínky na derivace. Mezi časté volby dodatečných podmínek patří
- předepíšeme hodnoty prvních derivací na krajích (přidáváme tak do úlohy další dva parametry, které musíme zvolit, nebo je necháme zadat uživatele) $f'_1(x_1) = \alpha$, $f'_{n-1}(x_n) = \beta$, nebo
- požadujeme, nulovost druhých derivací (graf na krajích interpolačního intervalu nebude vypouklý) $f''_1(x_1) = f''_{n-1}(x_n) = 0$.
Ukázky
Porovnání různých interpolací
Na závěr tohoto příspěvku ukážeme konkrétní příklad interpolace. Výše v textu jsme čtenáři pro ilustraci výkladu předložili obrázky 1 a 2. V obou případech jsme uvažovali čtyři body o souřadnicích \begin{align}\label{eq-body} A_1 &= (1.0, 1.25), & A_2 &= (2.0, 3.00), \\ A_3 &= (3.5, 0.50), & A_4 &= (5.0, 2.25). \nonumber \end{align} Ukažme si, jak v tomto konkrétním jednoduchém příkladě dopadne interpolace.
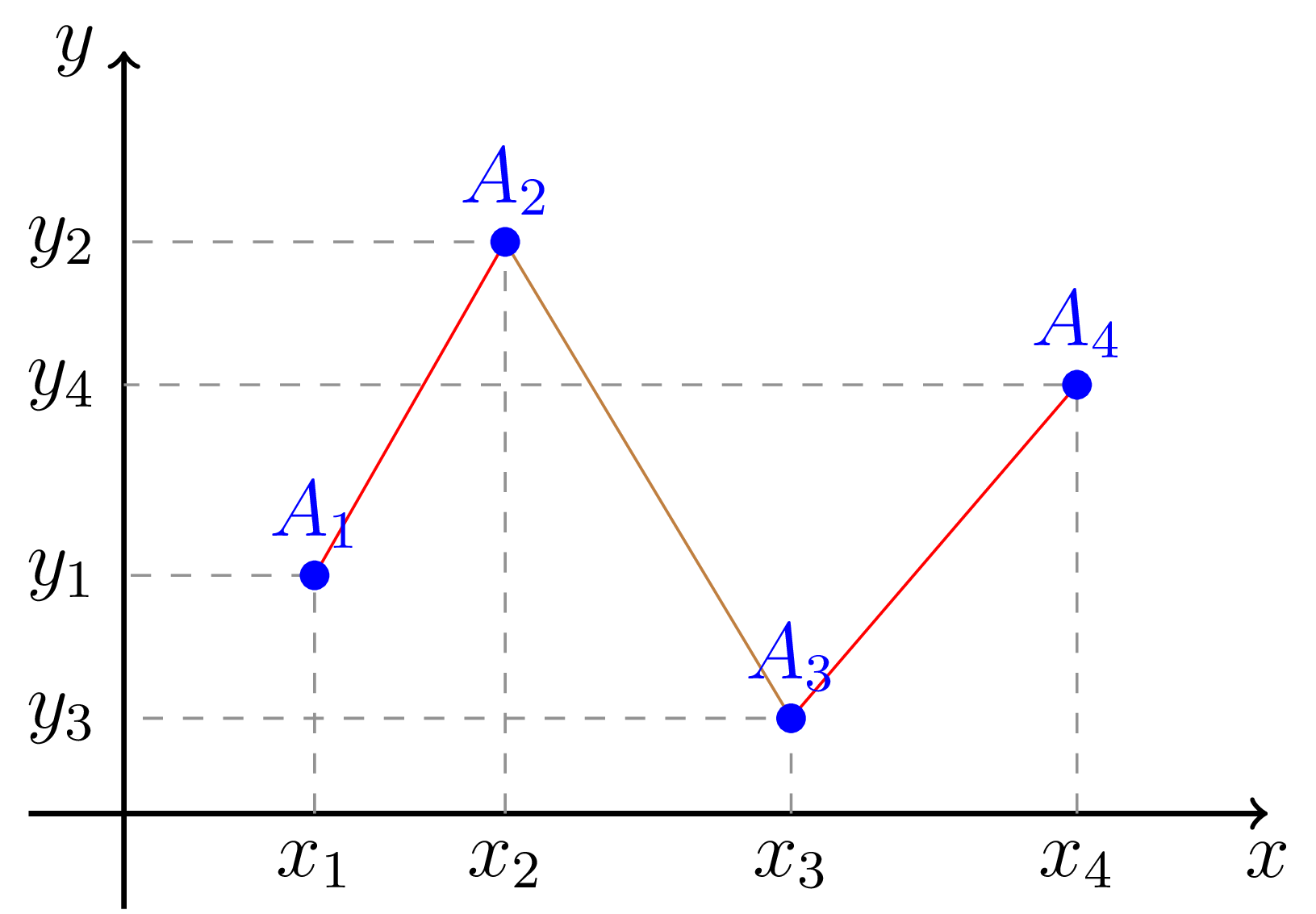
Obrázek č. 3: Lineární interpolace bodů \eqref{eq-body}. Ke spojení bodů využíváme grafy polynomů stupně $m=1$, tedy přímek.
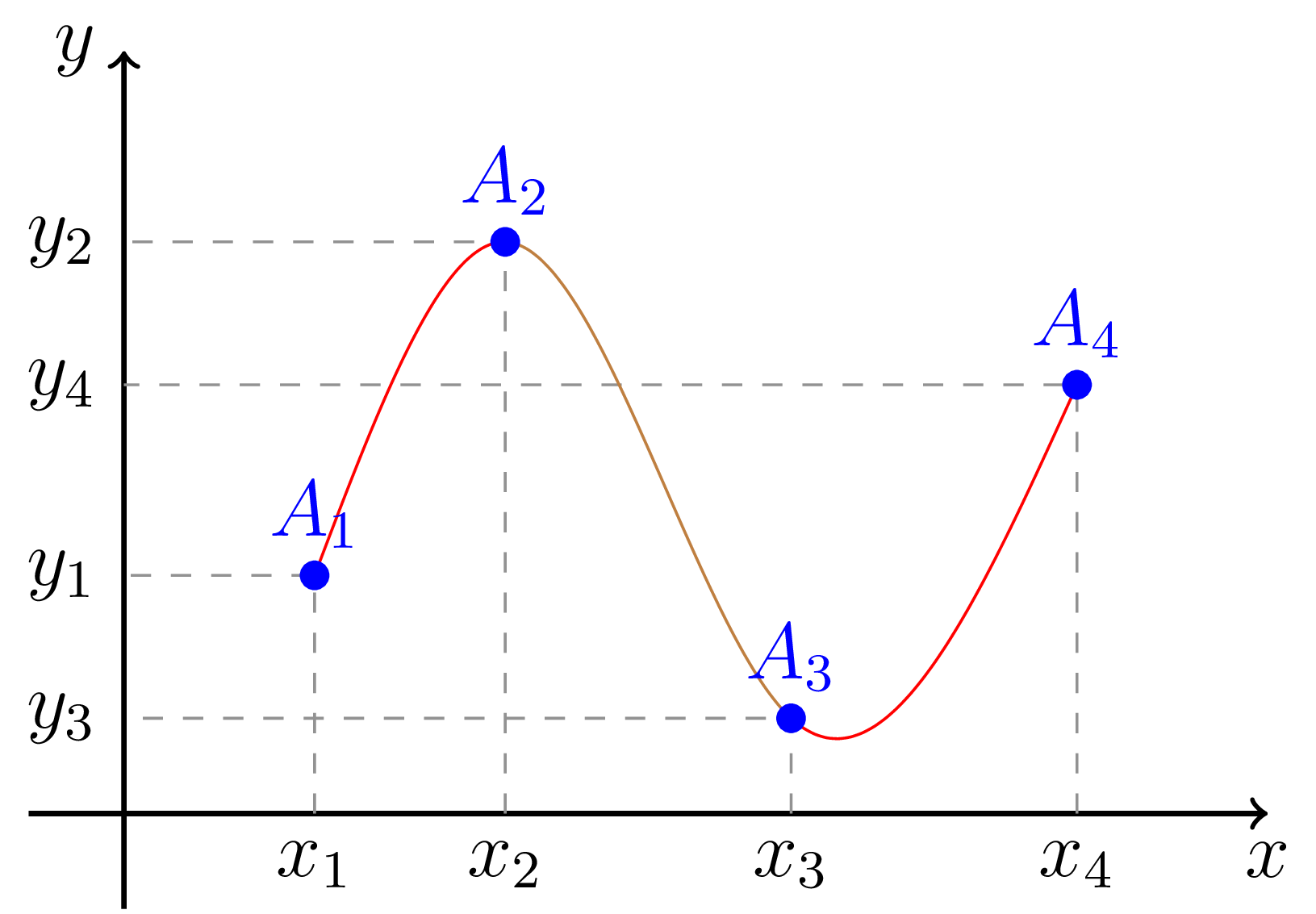
Obrázek č. 4: Kubická interpolace bodů \eqref{eq-body}. Body jsou spojeny grafy polynomů stupně $m=3$, na krajích navíc požadujeme nulovost druhých derivací.
Zjednodušená interaktivní ukázka
Často potřebujeme interpolovat pouze mezi dvěma body. Například bychom chtěli v textovém editoru pěkně vedle sebe znázornit změny v textu. Na toto jednoduché využití kubické interpolace můžeme narazit v řadě GUI programů pro správu změn kódu (Git, SVN). Na jedné straně okna se zobrazuje původní verze kódu, na druhé nová verze, a změněné části kódu jsou spojeny svorkou vytvořenou právě pomocí kubické interpolace.
Máme tedy zadány dva body $A_1 = (x_1, y_1)$ a $A_2 = (x_2, y_2)$. Interpolační úlohu uvedenou výše (s požadavkem nulových prvních derivací na krajích) lze explicitně vyřešit. Koeficienty kubického interpolačního polynomu \[ f(x) = a + bx + cx^2 + dx^3 \] jsou dány následovně \begin{align*} a &= \frac{3 x_1 x_2^2 y_1 - x_2^3 y_1 + x_1^3 y_2 - 3 x_1^2 x_2 y_2}{(x_1 - x_2)^3}, \\ b &= -\frac{6 x_1 x_2 (y_1 - y_2)}{(x_1 - x_2)^3}, \\ c &= \frac{3 (x_1 + x_2) (y_1 - y_2)}{(x_1 - x_2)^3}, \\ d &= -\frac{2 (y_1 - y_2)}{(x_1 - x_2)^3}. \end{align*}
Na následujícím obrázku můžete vertikálně posunovat oběma body a sledovat jak se pěkně kubický polynom mění (pokud demonstrace odmítá poslušnost, proveďte opakované načtení stránky, *reload*). Obdélníky na obou stranách pak symbolicky znázorňují starou a novou verzi kódu.
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).

