Chaos v jednoduchém dynamickém systému
Cílem tohoto příspěvku je demonstrovat existenci zajímavých a komplexních efektů i u na první pohled velmi elementárního matematického modelu tzv. logistického zobrazení. Navíc si ukážeme jednu z možných praktických aplikací tohoto modelu jakožto generátoru pseudonáhodných číselných posloupností.
Popis modelu
Uvažme následující rekurentně zadanou posloupnost \begin{equation} \label{eq-logistic} x_{n+1} = \alpha \cdot x_n \cdot (1 - x_n), \quad n = 0,1,2,\ldots \end{equation} s prvním členem (počáteční podmínkou) $x_0 \in (0,1)$ a parametrem $\alpha \in (0,4)$.
Tento příklad rekurentně zadané posloupnosti je pozoruhodný jednoduchostí svého zadání v protikladu k jeho chování, které popíšeme níže. Skutečně, k zadání posloupnosti si v rovnici \eqref{eq-logistic} vystačíme pouze s násobením čísel, žádná věda, dalo by se říci. Než se pustíte do čtení zbytku článku, zkuste se zamyslet a utvořit hypotézu o chování takovéto posloupnosti v závislosti na hodnotě $x_0$ a parametru $\alpha$.
Poznámka k motivaci
Výše uvedený model bývá uváděn pod jménem logistické zobrazení (*logistic map*). Původní motivací pro sestavení tohoto diskrétního matematického modelu je popis populační dynamiky. Zvídavý čtenář se může více dozvědět na wikipedii a zejména pak odkazech tamtéž, případně v obsáhlé knížce [2].
Pro nás je tento model atraktivní svou jednoduchostí a zajímavým chováním. Na závěr tohoto článku si ukážeme jednu z jeho aplikací jakožto základu pro *generátor pseudonáhodných číselných posloupností*. Jak už tomu bývá v matematice zvykem, tato aplikace nemá pranic společného s původní motivací pro studium tohoto modelu.
Chování posloupnosti
Pojďme zábavnou experimentální formou využívající počítač prozkoumat chování posloupnosti \eqref{eq-logistic}.
Průzkum vlastností
Za výše uvedených předpokladů (pro jistotu je zopakujeme: $x_0 \in (0,1)$, $\alpha \in (0,4)$) jsou všechny členy posloupnosti \eqref{eq-logistic} z intervalu $(0,1)$. Skutečně, označme si funkci \[ f_\alpha(x) := \alpha \cdot x \cdot (1 - x). \] Jejím grafem je parabola. Průsečíky s osou $x$ má zřejmě v bodech $(0,0)$ a $(1,0)$. Vrchol této paraboly je v bodě o souřadnicích $\left(\frac{1}{2}, \frac{\alpha}{4}\right)$. Pro všechna $x$ z intervalu $(0,1)$ proto platí nerovnosti \[ 0 < f_\alpha(x) \leq f_\alpha\left(\frac{1}{2}\right) = \frac{\alpha}{4} < \frac{4}{4} = 1. \] Pro ilustraci uvádíme názorný obrázek 1. Uvědomíme-li si, že rekurentní vztah \eqref{eq-logistic} lze pomocí funkce $f_\alpha$ přepsat do tvaru \begin{equation} \label{eq-f-alpha} x_{n+1} = f_\alpha(x_n), \quad n=0,1,2,\ldots \end{equation} a že předpokládáme $x_0 \in (0,1)$, pak ihned matematickou indukcí ověříme, že skutečně $x_n \in (0,1)$ pro každé $n \in \mathbb{N}_0$.
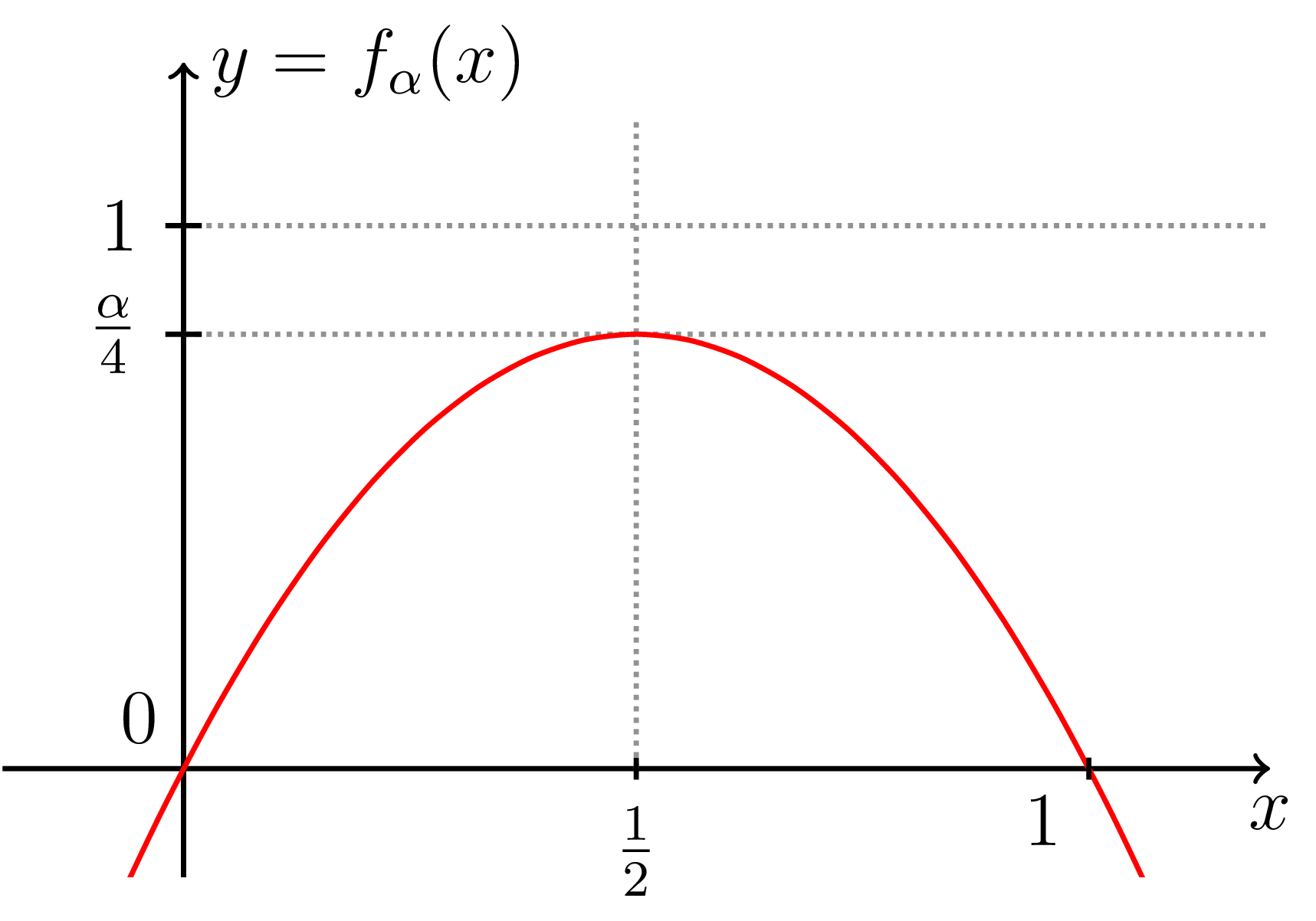
Obrázek č. 1: Graf kvadratické funkce $f_\alpha(x) = \alpha \cdot x \cdot (1-x)$ pro $\alpha \in (0,4)$ nad intervalem $\langle 0,1 \rangle$.
Poznámka k úhlu pohledu
Na rekurenci \eqref{eq-logistic} lze pohlížet jako na tzv. diskrétní dynamický systém na intervalu $(0,1)$. Pokusme se tuto terminologii stručně ozřejmit (zájemce odkazujeme na [2]). Funkce $f_\alpha$ zobrazuje interval $(0,1)$ opět do intervalu $(0,1)$ a člen naší posloupnosti \eqref{eq-logistic} lze získat iterací této funkce, tj. platí \[ x_n = f_\alpha^{n}(x_0), \] kde $f_\alpha^0 = \mathrm{id}$ (identické zobrazení) a $f_\alpha^n = f_\alpha \circ \cdots \circ f_\alpha$ ($n$ složených funkcí). Každá aplikace zobrazení $f_\alpha$ zde reprezentuje jeden (diskrétní) časový krok. Hodnota $x_n$ tedy představuje stav systému v čase $n$ jak se vyvinula z počátečního stavu $x_0$. Tento pohled na věc demonstruje následující obrázek 2.
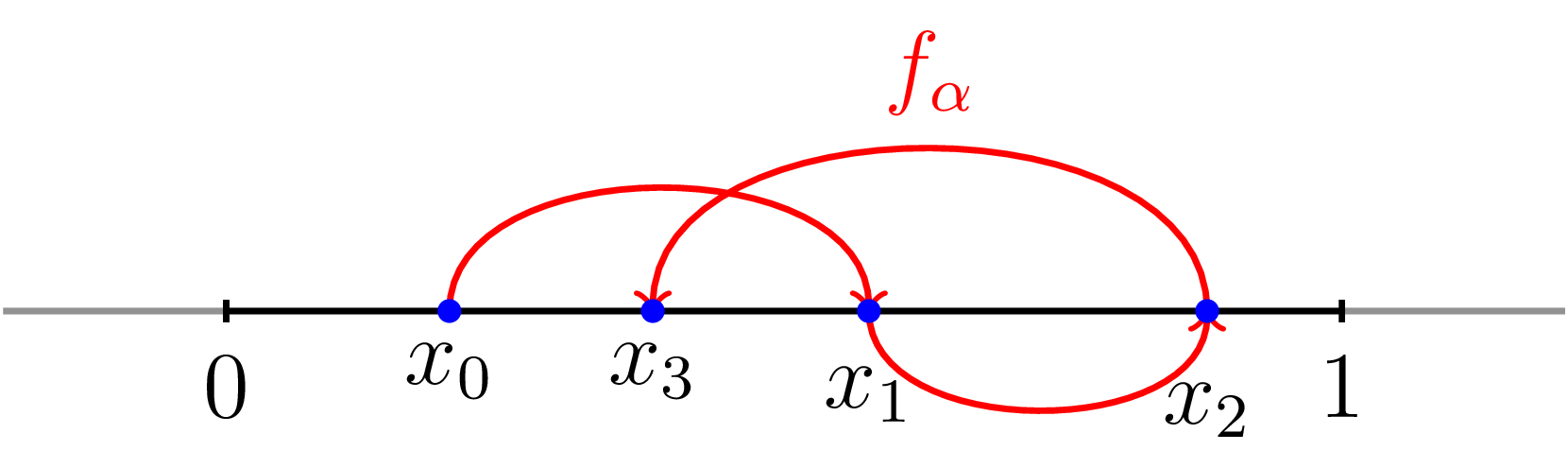
Obrázek č. 2: Funkce $f_\alpha$ zobrazuje interval $(0,1)$ do intervalu $(0,1)$ a její opakovanou aplikací tak získáváme diskrétní dynamický systém. Můžete si představovat jak funkce $f_\alpha$ posunuje počáteční bod $x_0$ po intervalu $(0,1)$.
Numerické experimenty
Pojďme se pomocí počítače pokusit zjistit, jak se chovají rekurentně zadané posloupnosti definované vzorcem \eqref{eq-logistic} v závislosti na parametru $\alpha$.
Zkusme nejprve namátkou třeba $\alpha = 0{,}4$ a tři různé počáteční hodnoty $x_0$. Prvních několik členů zachycuje následující tabulka.
| $x_0 = 0{,}6$ | $x_0 = 0{,}5$ | $x_0 = 0{,}3$ | |||
|---|---|---|---|---|---|
| $n$ | $x_n$ | $n$ | $x_n$ | $n$ | $x_n$ |
| 0 | 0,6 | 0 | 0,5 | 0 | 0,3 |
| 1 | 0,096 | 1 | 0,1 | 1 | 0,08399999999999999 |
| 2 | 0,034713600000000004 | 2 | 0,03600000000000001 | 2 | 0,0307776 |
| 3 | 0,013403426390016002 | 3 | 0,013881600000000004 | 3 | 0,011932135735296001 |
| 4 | 0,00528950982040937 | 4 | 0,005475560472576002 | 4 | 0,00471590394883619 |
| 5 | 0,002104612362507665 | 5 | 0,002178231484034866 | 5 | 0,0018774656795126166 |
| 6 | 0,0008400731877244979 | 6 | 0,0008693947166547302 | 6 | 0,0007495763208539476 |
| 7 | 0,0003357469859055058 | 7 | 0,0003474555477925532 | 7 | 0,00029960578247726515 |
| 8 | 0,00013425370394678447 | 8 | 0,00013893392897394456 | 8 | 0,00011980640754094855 |
| 9 | 5,3694271955904415e-5 | 9 | 5,556585053492977e-5 | 9 | 4,791682158626427e-5 |
| 10 | 2,1476555552425416e-5 | 10 | 2,2225105188473642e-5 | 10 | 1,916581022578934e-5 |
| 11 | 8,590437723994808e-6 | 11 | 8,889844493269201e-6 | 11 | 7,666177159003094e-6 |
| 12 | 3,4361455713498075e-6 | 12 | 3,5559061855736344e-6 | 12 | 3,0664473554923446e-6 |
| 13 | 1,3744535057013682e-6 | 13 | 1,4223574164419335e-6 | 13 | 1,2265751809571845e-6 |
| 14 | 5,497806466315715e-7 | 14 | 5,689421573365253e-7 | 14 | 4,90629470588204e-7 |
Zdá se, že ať volíme počáteční podmínku $x_0$, jak chceme, tak vzniknuvší posloupnost konverguje k $0$. Po chvilce zamyšlení by toto pozorování nemělo být překvapivé. Z rekurentního vztahu totiž plyne odhad \[ 0 < x_{n+1} < \alpha x_n, \quad n = 0,1,2,\ldots \] Je-li tedy $\alpha$ menší než $1$, pak naše posloupnost klesá k nule ne pomaleji než geometrická posloupnost s kvocientem $\alpha$ (kladným a menším než jedna).
Co se děje pro ostatní hodnoty $\alpha$? Takto suše se chovající posloupnost bychom si zde asi nerozebírali. Zkusme experiment zopakovat s hodnotou větší než $1$. Zvolme zkusmo $\alpha = 1{,}4$ a opět tři různé počáteční hodnoty. Výsledky experimentu jsou opět zaneseny v následující tabulce.
| $x_0 = 0{,}7$ | $x_0 = 0{,}5$ | $x_0 = 0{,}1$ | |||
|---|---|---|---|---|---|
| $n$ | $x_n$ | $n$ | $x_n$ | $n$ | $x_n$ |
| 0 | 0,7 | 0 | 0,5 | 0 | 0,1 |
| 1 | 0,294 | 1 | 0,35 | 1 | 0,126 |
| 2 | 0,29058959999999995 | 2 | 0,31849999999999995 | 2 | 0,1541736 |
| 3 | 0,288606198120576 | 3 | 0,3038808499999999 | 3 | 0,182565741488256 |
| 4 | 0,2874377247377479 | 4 | 0,29615219060458847 | 4 | 0,208929688132339 |
| 5 | 0,2867441907894684 | 5 | 0,29182449884656875 | 5 | 0,2313893029689676 |
| 6 | 0,2863307437731459 | 6 | 0,28932814500732484 | 6 | 0,2489876108167041 |
| 7 | 0,28608362852084807 | 7 | 0,28786431731952333 | 7 | 0,261789892667091 |
| 8 | 0,28593570041847083 | 8 | 0,28699783298716336 | 8 | 0,27055832267022156 |
| 9 | 0,28584706590253706 | 9 | 0,2864821075869699 | 9 | 0,276299123385737 |
| 10 | 0,28579392914442675 | 10 | 0,2861741534672968 | 10 | 0,27994108492281433 |
| 11 | 0,285762062892064 | 11 | 0,28598991029640203 | 11 | 0,2822037034530728 |
| 12 | 0,2857429488252305 | 12 | 0,2858795541070811 | 12 | 0,2835906824946201 |
| 13 | 0,28573148243064905 | 13 | 0,2858134085108646 | 13 | 0,28443381021559794 |
| 14 | 0,2857246033300858 | 14 | 0,28577374563677277 | 14 | 0,2849437049505692 |
Z uvedených několika prvních členů tří posloupností s různými počátečními podmínkami získáváme dojem, že nezávisle na volbě počáteční podmínky posloupnosti konvergují vždy ke stejné limitě, jejíž hodnota je přibližně rovna $0{,}28$. Zvídavý a skeptický čtenář může pro $\alpha = 1{,}4$ zkusit jiné počáteční podmínky a více členů.
Můžeme experimentovat dál a zkusit například $\alpha = 2{,}4$. Podobným způsobem jako výše získáme dojem, že nezávisle na volbě počáteční podmínky posloupnosti s tímto $\alpha$ konvergují k limitě, jejíž hodnota je přibližně rovna $0{,}58$.
Zdá se, že se vzrůstající hodnotou $\alpha$ všechny posloupnosti konvergují k limitě nezávislé na $x_0$ a tato limitní hodnota postupně roste (nejprve je jistou dobu $0$ a pak se postupně zvětšuje). (Hlubší analýzou bychom mohli zjistit, že toto tvrzení je opravdu pravdivé. Lze dokázat, že pro $\alpha \in \langle 1,3\rangle$ je jediným hromadným bodem těchto posloupností $(\alpha - 1) / \alpha$.)
Hodnotu $\alpha$ máme shora omezenou číslem $4$ a proto jsme doposud zdaleka neprozkoumali všechny možnosti. Zkusme se opět stejným způsobem jako výše podívat na hodnotu $\alpha = 3{,}4$. Naše pokusy jsou shrnuty v následující tabulce.
| $x_0 = 0{,}7$ | $x_0 = 0{,}45$ | $x_0 = 0{,}2$ | |||
|---|---|---|---|---|---|
| $n$ | $x_n$ | $n$ | $x_n$ | $n$ | $x_n$ |
| 0 | 0,7 | 0 | 0,45 | 0 | 0,2 |
| 1 | 0,7140000000000001 | 1 | 0,8415000000000001 | 1 | 0,544 |
| 2 | 0,6942936 | 2 | 0,4534843499999997 | 2 | 0,8434176 |
| 3 | 0,7216499897967361 | 3 | 0,8426434006372635 | 3 | 0,449018796834816 |
| 4 | 0,682962358878563 | 4 | 0,4508246999990879 | 4 | 0,8411631175410227 |
| 5 | 0,7361842357942124 | 5 | 0,841778085557389 | 5 | 0,4542662725809471 |
| 6 | 0,6603378229918331 | 6 | 0,45283831679126874 | 6 | 0,8428886489996231 |
| 7 | 0,7625920605620147 | 7 | 0,8424376371655256 | 7 | 0,45025307291652505 |
| 8 | 0,6155543930813037 | 8 | 0,4513039798184723 | 8 | 0,8415858270355548 |
| 9 | 0,8046004196146793 | 9 | 0,8419375719028328 | 9 | 0,4532850174126824 |
| 10 | 0,5345431868599083 | 10 | 0,45246756953206313 | 10 | 0,8425802153663466 |
| 11 | 0,8459430120213088 | 11 | 0,8423182713829566 | 11 | 0,4509719065344617 |
| 12 | 0,4430996702743235 | 12 | 0,4515818836631073 | 12 | 0,841827236573857 |
| 13 | 0,8389919984221715 | 13 | 0,8420293324353162 | 13 | 0,4527240771433532 |
| 14 | 0,45928704501952433 | 14 | 0,4522541815630967 | 14 | 0,8424009562013781 |
Pozor! To je nové chování! Z výše uvedeného experimentu se zdá, že nezávisle na hodnotě $x_0$ nyní příslušná posloupnost není konvergentní, ale má dva různé hromadné body. Jeden blízko $0{,}4$ a druhý blízko $0{,}8$!
Vizualizace chování
Zkusme se pokusit situaci analyzovat graficky. Sáhodlouhé tabulky nejsou příliš efektivní a názorné. Napíšeme jednoduchý kód, který se bude snažit (v dané přesnosti) určit všechny hromadné body zadané posloupnosti a pomocí tohoto kódu se podíváme na posloupnosti vzniknuvší pro $\alpha \in \langle 2{,}4, 3{,}4\rangle$.
Popsaná situace je znázorněna na následujícím obrázku 3.
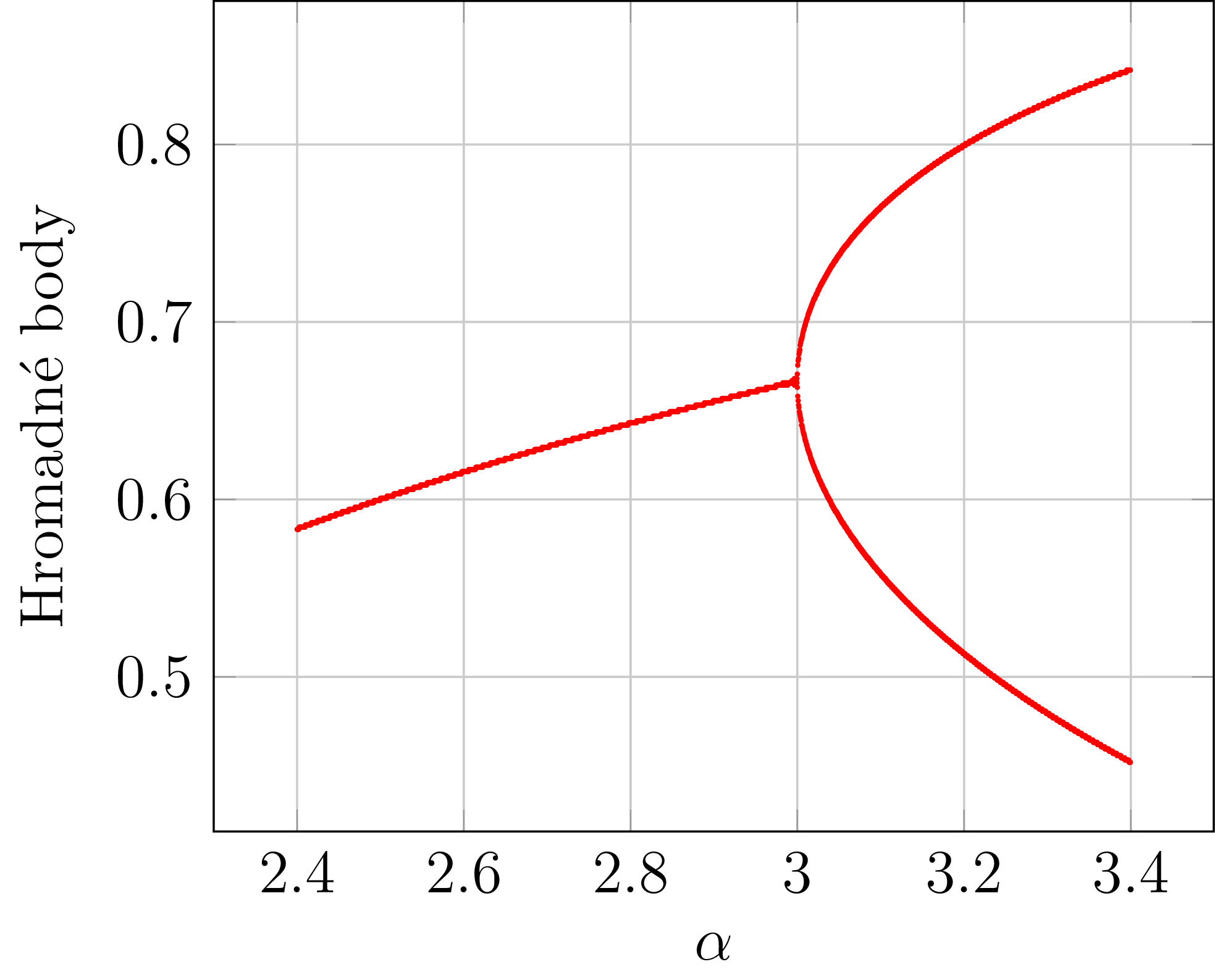
Obrázek č. 3: Hromadné body posloupností \eqref{eq-logistic} v závislosti na $\alpha \in \langle 2{,}4, 3{,}4 \rangle$. Pozorujeme kvalitativní změnu chování, tzv. bifurkaci.
Tato kvalitativní změna chování (nejprve měly posloupnosti právě jeden hromadný bod (byly konvergentní) a při plynulém přechodu parametru do jiné oblasti mají najednou dva různé hromadné body) se v teorii dynamických systémů nazývá bifurkace.
Co se děje dál? Se zvyšujícím se parametrem $\alpha$ dochází k dalšímu rozdělení a pro $\alpha = 3{,}5$ mají posloupnosti dokonce již čtyři hromadné body. Toto chování ukazuje následující obrázek 4.
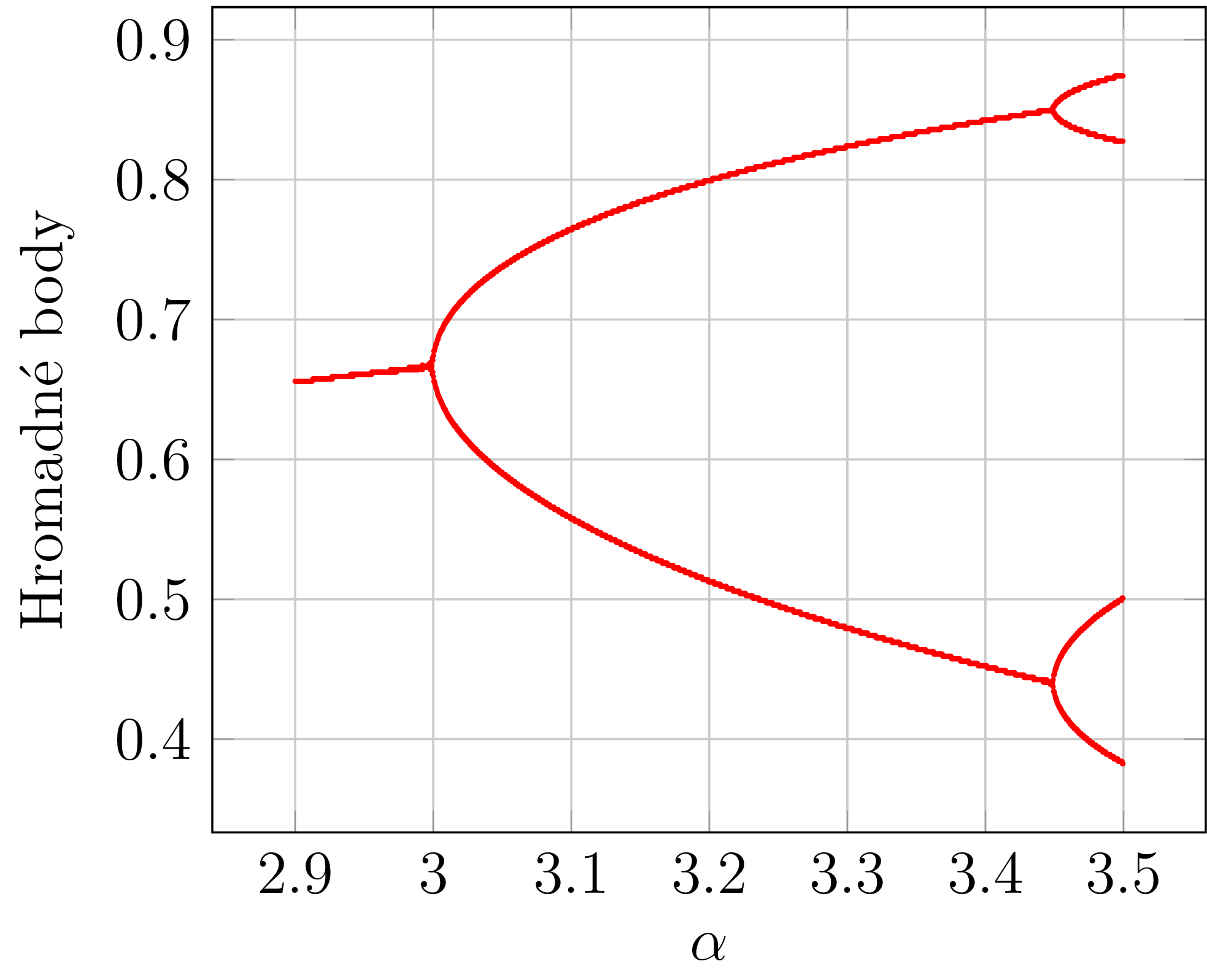
Obrázek č. 4: Hromadné body posloupností \eqref{eq-logistic} v závislosti na $\alpha \in \langle 2{,}9, 3{,}5 \rangle$.
Podívejme se konečně na tento (tzv. bifurkační diagram) v celé jeho kráse na obrázku 5. Tedy alespoň pro zajímavou část parametrů $\alpha$. Vidíme, že chování je čím dál tím exotičtější. Pro některé parametry nemají posloupnosti konečný počet hromadných bodů, ale jejich hromadné body pokrývají celé intervaly.
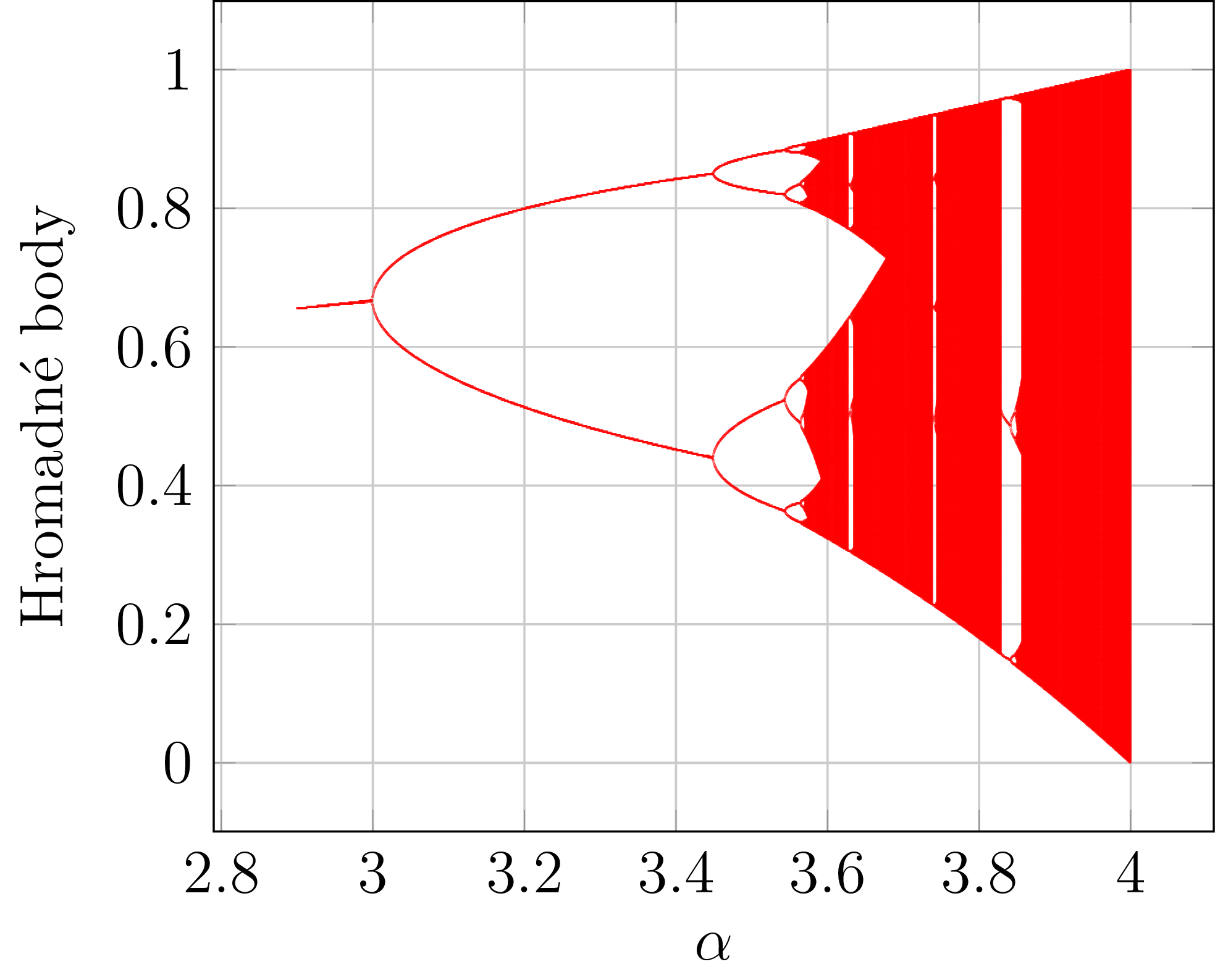
Obrázek č. 5: Hromadné body posloupností \eqref{eq-logistic} v závislosti na $\alpha \in \langle 2{,}8, 4 \rangle$.
V hraniční situaci $\alpha = 4$ tento systém vykazuje chaotické chování. Množina hromadných bodů posloupností \eqref{eq-logistic} je pro tuto hodnotu parametru celý interval $\langle 0,1 \rangle$. Navíc vezmeme-li dvě posloupnosti s velmi blízkými počátečními podmínkami, pak se jejich vzdálenost bude postupně dramaticky zvětšovat (to je jedna z možných definic klasického chaosu).
Generátor pseudonáhodné posloupnosti čísel
Chaotického chování uvedeného v předcházející části textu si všimli autoři článku [1] a pokusili se ho využít ke konstrukci generátoru pseudonáhodných číselných posloupností.
Představme si, že chceme generovat náhodnou posloupnost čísel například z intervalu $\langle 0,1 \rangle$. Skutečně náhodná posloupnost musí být (mimo jiné) nereprodukovatelná. Toho lze dosáhnout využitím různých fyzikálních efektů (detekce částic vesmírného záření, radioaktivní rozpad, tepelný šum v elektrických zařízeních, atp.) Takovýto generátor je ale komplikované provozovat a navíc náhodná čísla nemusí generovat dostatečně rychle. Obzvlášť v dnešní době navíc nemusí být periferie počítače se zdrojem radioaktivního záření úplně nejžádanější.
V praxi se používá pseudonáhodných generátorů. To jsou deterministické algoritmy generující posloupnosti čísel co nejvíce připomínající skutečně náhodné posloupnosti čísel. Tyto posloupnosti jsou ale reprodukovatelné, známe-li parametry generátoru a tzv. *seed*.
Čtenáři je teď asi jasné, jakým způsobem využijeme posloupnosti \eqref{eq-logistic}. Parametr $\alpha$ zvolíme roven $4$ (pro ostatní hodnoty by jistě nešlo o dobrý generátor čísel z $\langle 0,1 \rangle$). Počáteční hodnota $x_0$ pak představuje *seed*. Stejná počáteční podmínka (stejný *seed*) nám dá stejnou pseudonáhodnou posloupnost čísel.
Je takto vytvořený generátor opravdu dobrý? Dává opravdu dobrou pseudonáhodnou posloupnost? Na tomto místě se nebudeme zabývat všemi detaily, zvídavého čtenáře odkazujeme na původní článek [1]. (Do úvahy je potřeba i vzít jaký datový typ používáme.) Ukažme si alespoň základní požadavek na pseudonáhodný generátor: rovnoměrnost rozdělení náhodně generovaných čísel.
Proveďme opět experiment, kdy si interval $\langle 0,1 \rangle$ rozdělíme na jistý počet $n_{\mathrm{bin}}$ stejně velkých přihrádek a vygenerujme jednu dlouhou posloupnost pomocí vzorce \eqref{eq-logistic} a jisté počáteční podmínky $x_0$ s $\alpha = 4$. Dále si zaznamenejme kolikrát členy této posloupnosti padnou do té které přihrádky. Tyto počty na závěr vydělme celkovým počtem námi napočtených členů této posloupnosti. Získáme tak odhad pravděpodobnosti, že člen posloupnosti padne do té které přihrádky. U dobrého náhodného generátoru požadujeme, aby tato pravděpodobnost byla stejná pro všechny přihrádky.
Pro naší posloupnosti \eqref{eq-logistic} získáme následující obrázek 6.
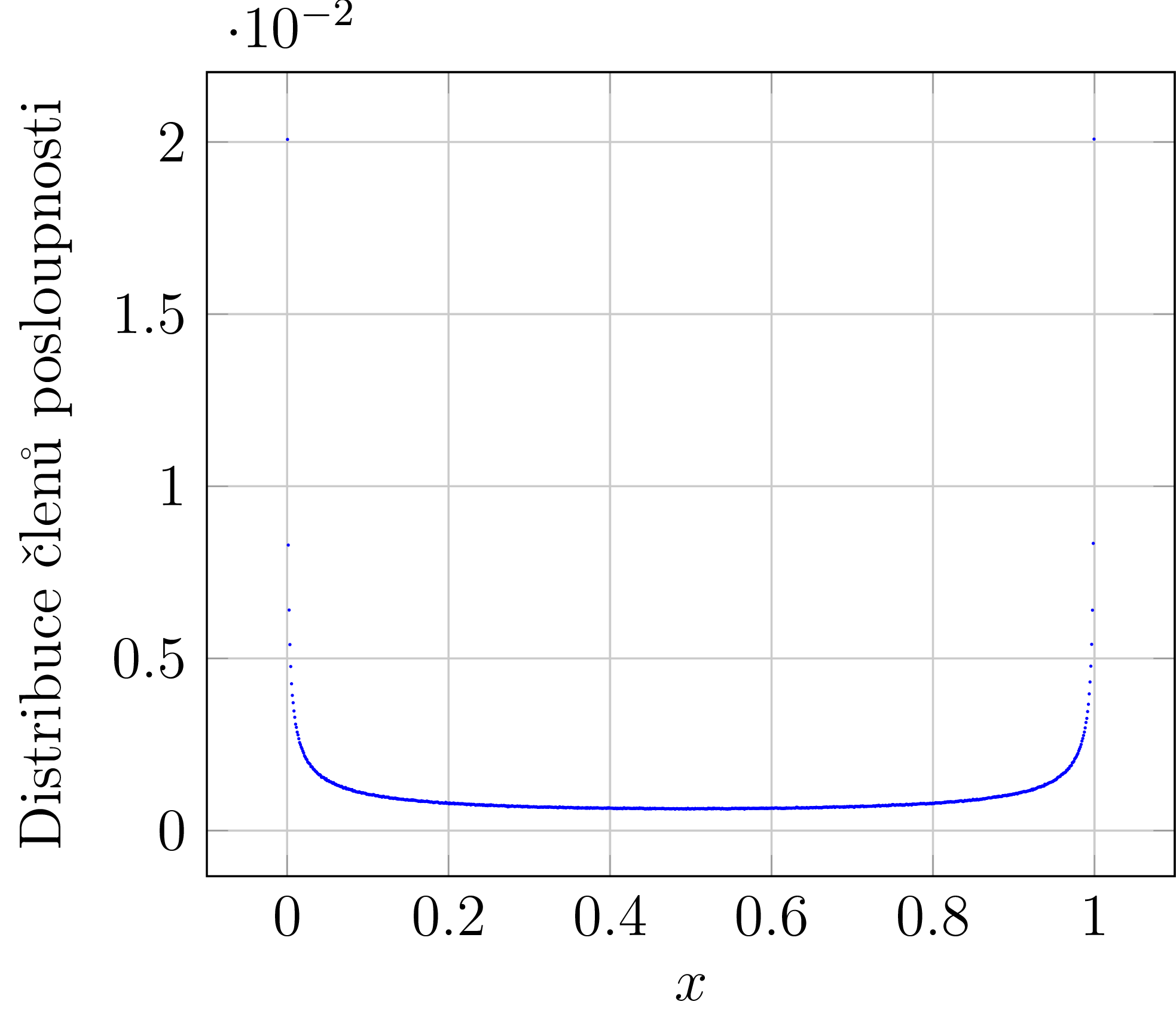
Obrázek č. 6: Distribuce členů posloupnosti $(x_n)_{n=0}^\infty$ s parametrem $\alpha = 4$. Interval $\langle 0,1 \rangle$ byl rozdělen na $n_{\mathrm{bin}} = 1000$ přihrádek, vygenerovaná posloupnost měla $50\,000\,000$ členů, počáteční podmínkou (seed) byl $x_0 = 0{,}3$ a výpočet jsme provedli pomocí 64 bitového floatu.
Výsledek na obrázku 6 se nám samozřejmě nelíbí. Vidíme, že generátor preferuje čísla blízká nule a jedničce. Funkční závislost grafu na obrázku 6, je úměrná $1/\sqrt{x \cdot (1-x)}$. To nám umožňuje náhodný generátor snadno opravit, abychom získali rovnoměrné rozdělení náhodných čísel.
Budeme počítat posloupnost $(x_n)_{n=0}^\infty$ tak, jak je uvedeno ve vzorci \eqref{eq-logistic}, ale uživateli nebudeme vracet $x_n$, ale číslo napočtené podle vzorce \[ y_n = \frac{1}{\pi} \mathrm{arccos} (1-2x_n), \quad n=0,1,2,\ldots \] Tj. posloupnost $(x_n)_{n=0}^\infty$ je pomocná posloupnost, kdežto $(y_n)_{n=0}^\infty$ je onou hledanou pseudonáhodnou posloupností. Distribuce, či rozložení, členů této posloupnosti v intervalu $(0,1)$ je znázorněna na následujícím obrázku 7
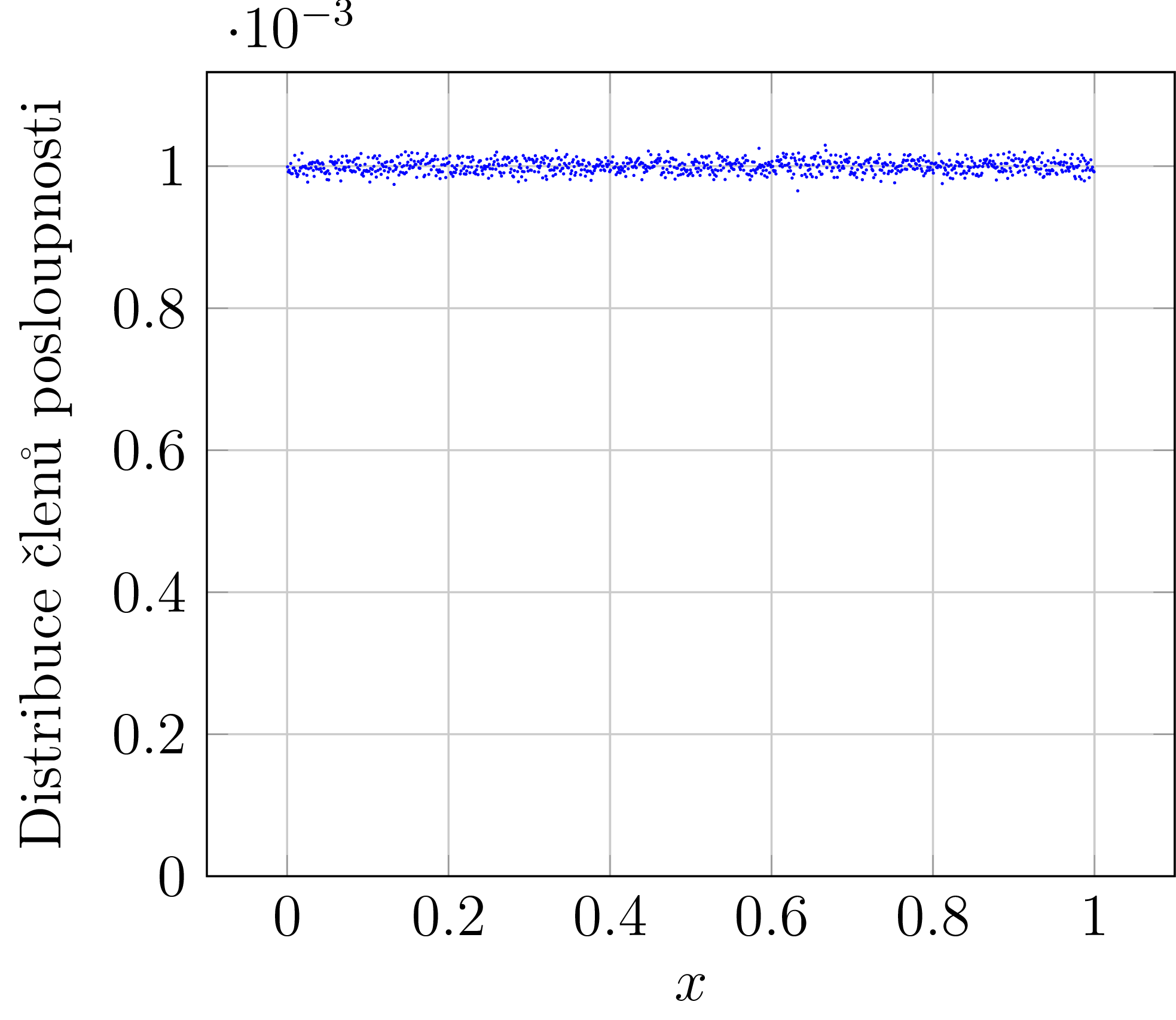
Obrázek č. 7: Distribuce členů posloupnosti $(y_n)_{n=0}^\infty$ s parametrem $\alpha = 4$. Interval $\langle 0,1 \rangle$ byl rozdělen na $n_{\mathrm{bin}} = 1000$ přihrádek, vygenerovaná posloupnost měla $50\,000\,000$ členů, počáteční podmínkou (seed) byl $x_0 = 0{,}3$ a výpočet jsme provedli pomocí 64 bitového floatu.
S tímto výsledkem jsme již spokojeni. Poznamenejme, že takovouto pseudonáhodnou posloupnost jsme schopni vytvořit pomocí relativně elementárních prostředků (sčítání, násobení, výpočet funkce $\mathrm{arccos}$). Aby tento generátor byl skutečně kvalitní, je potřeba implementaci ještě dále vyladit. Detaily čtenář může získat z již uvedeného článku [1].
Literatura
- Phatak, S.C. a Suresh Rao, S., Logistic map: A possible random-number generator, Physical Review E, 1995, Vol. 51, No. 4, pp. 3670-3678
- Kůrka, P., Topological and Symbolic Dynamics, Cours specialisés, SMF, 2007
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).

