Sdílení tajemství pomocí polynomiální interpolace
Jak bezpečně rozdělit utajenou informaci skupině lidí tak, aby ji byli schopni zrekonstruovat jen tehdy, sejde-li se jich dostatečný počet? Shamirovo schéma umožňuje problém řešit efektivně pomocí polynomiální interpolace.
Schémata sdílení tajemství umožňují $n$ podílníkům sdílet utajenou informaci reprezentovanou číslem $N\in\mathbb{Z}$ tak, že
$N$ lze jednoznačně určit sejde-li se alespoň $k$ podílníků.
sejde-li se nejvýše $k-1$ podílníků, nezjistí o $N$ více než někdo, kdo žádný podíl na sdíleném tajemství nemá.
V příspěvku Bezpečné sdílení tajemství s využitím soustav lineárních rovnic jsme představili motivaci pro vytvoření systému sdílení tajemství a také požadavky, které musí systém splňovat. Viděli jsme, že utajené $N$ může představovat GPS souřadnice pokladu nebo soukromý klíč šifrovacího systému RSA. Seznámili jsme se také s Blakleyho schématem [1], které využívá sdílení soustav lineárních rovnic pro $k$ proměnných nad konečným tělesem $\mathbb{Z}_p$ zvoleným tak, aby prvočíslo $p$ bylo větší než $N$. Pracujeme-li v $\mathbb{Z}_p$, kde $N$ a $p$ jsou $b$-bitová čísla, musíme očekávat, že každý z koeficientů vystupujících v lineárních rovnicích bude opět $b$-bitové číslo. Pro uchování jedné rovnice je potřeba $(k+1)b$ bitů, což může znamenat velký objem dat. Systém navržený nezávisle A. Shamirem v článku [2] využívá polynomiální interpolace a je v tomto ohledu mnohem efektivnější, přestože jsou obě schémata v základu ekvivalentní.
Interpolace polynomu
Je známo, že polynom $p(x)$ stupně nejvýše $k-1$ ve tvaru \[ p(x)=a_0 + a_1 x + a_2 x^2 + \ldots + a_{k-1} x^{k-1}, \qquad a_j \in \mathbb{R},\ j\in\{0,\ldots,k-1\} \] lze jednoznačně určit, pokud známe funkční hodnoty $y_i$ polynomu $p(x)$ v $k$ různých bodech $x_i$. Jinými slovy, $p(x)$ je možno zadat pomocí $k$ bodů \[ A_i=(x_i,y_i)\in\mathbb{R}^2,\qquad i\in\{1,\ldots,k\}, \] pro které platí, že \[ p(x_i)=y_i, \] a zároveň $x_i\neq x_j \text{ pro } i\neq j$. Koeficienty $a_j$ polynomu $p(x)$ lze nalézt jako řešení soustavy $k$ lineárních rovnic \begin{equation}\label{soustava_interpolace} \begin{matrix} a_{0} & + & a_{1}x_1 & + & \cdots & + & a_{k-1}x_1^{k-1} & = & y_1, \\ \vdots & & \vdots & & \ddots & & \vdots & & \vdots \\ a_{0} & + & a_{1}x_k & + & \cdots & + & a_{k-1}x_k^{k-1} & = & y_k \end{matrix} \end{equation} pro $k$ neznámých $a_0, \ldots, a_{k-1}$.
Příklad 1
Pro ilustraci vyberme stejně jako na obrázku 1 čtyři body (pro lepší čitelnost zde píšeme místo desetinné čárky tečku) \begin{equation}\label{interpolace_body} A_1=(-1,-1), \quad A_2=\left(0.5, 0.5\right), \quad A_3=(1,0), \quad A_4=\left(1.5 , 2\right). \end{equation}
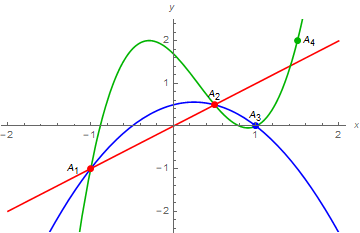
Obrázek 1: Body $A_1$ a $A_2$ určují jednoznačně přímku. Body $A_1, A_2$ a $A_3$ určují jednoznačně parabolu. Body $A_1, A_2, A_3$ a $A_4$ jednoznačně zadávají kubickou křivku.
Jak vidno, dva body $A_1$ a $A_2$ jednoznačně zadávají přímku která jimi prochází, a která představuje graf polynomu $p_1 (x) = x$. Body $A_1, A_2$ a $A_3$ neleží na jedné přímce a proto jednoznačně určují parabolu, která je grafem funkce $p_2 (x) = -x^2 + \frac{1}{2}x +\frac{1}{2}$. K nalezení koeficientů kubického polynomu \[ p_3(x)=a_0 + a_1 x + a_2 x^2 +a_3 x^3 \] jehož graf prochází body $A_1, A_2, A_3$ a $A_4$ je potřeba řešit soustavu lineárních rovnic \begin{equation*} \begin{matrix} a_0 & + & a_1 (-1) & + & a_2 (-1)^2 & + & a_3 (-1)^3 & = & -1,\\ a_0 & + & a_1 \left(0.5\right) & + & a_2 \left(0.5\right)^2 & + & a_3\left(0.5\right)^3 & = & 0.5,\\ a_0 & + & a_1 (1) & + & a_2(1)^2 & + & a_3(1)^3 & = & 0,\\ a_0 & + & a_1\left(1.5\right)& + & a_2\left(1.5\right)^2 & + & a_3\left(1.5 \right)^3 & = & 2. \end{matrix} \end{equation*} Nalezneme-li řešení zjistíme, že hledaný polynom $p_3(x)$ má tvar \[ p_3(x)=\frac{1}{10}( 17 - 19 x - 22 x^2 + 24 x^3). \] K určení $p_3(x)$ bylo nutno zadat všechny čtyři body $A_i, i\in\{1,\ldots,4\}$, neboť existuje nekonečně mnoho kubických křivek procházejících třemi body $A_1, A_2, A_3$. Na grafu kubické křivky lze ale zadat libovolný počet bodů, přičemž každé čtyři body ji jednoznačně určují. Toho lze výhodně využít při konstrukci schématu sdílení tajemství.
Shamirovo schéma
A. Shamir v článku [2] navrhl pro vytvoření podílů na sdíleném tajemství náhodně zvolit polynom $p(x)=a_0 + \ldots + a_{k-1} x^{k-1}$ tak, že koeficient $a_0$ bude roven sdílené informaci $N$. Jednotlivé podílníky je pak třeba očíslovat, spočíst funkční hodnoty polynomu $p(x)$ v $n$ bodech \[ y_1=p(1), \quad y_2=p(2), \quad \ldots ,\quad y_n=p(n) \] a $i$-tému podílníkovi předat bod $A_i=(i,y_i)$, $i\in\{1,\ldots,n\}$. Sejde-li se $k$ podílníků, sestaví ze svých podílů rovnice \eqref{soustava_interpolace}, kde $x_i=i$. Vyřešením soustavy rovnic naleznou sdílené tajemství $N=a_0$. Stejně jako u Blakleyho schématu tedy bezpečnost Shamirova schématu závisí na schopnosti nalézt řešení jisté soustavy lineárních rovnic. Je-li k dispozici méně než $k$ podílů, řešení nelze jednoznačně určit.
Podobně jako v Blakleyho schématu je i v Shamirově přístupu výhodnější pracovat s konečným tělesem $\mathbb{Z}_p$. Zvolíme tedy prvočíslo $p$ takové že $N<p$ a náhodně vybereme polynom \[ p(x)=a_0 + a_1 x + \ldots + a_{k-1} x^{k-1}, \quad a_0=N,\quad a_j \in \mathbb{Z}_p,\ j\in\{0,\ldots,k-1\}. \] Funkční hodnoty polynomu $y_i=p(i)$ distribuované podílníkům nyní počítáme modulo $p$. Abychom mohli spočíst hodnoty $p(x)$ v $n$ různých bodech, je také nutné aby $n<p$. Hodnotu v bodě $i=0$ přitom nelze distribuovat, neboť $p(0)=a_0=N$. Je-li pro zápis $p$ ve dvojkové soustavě potřeba $b$-bitů, očekáváme, že i $y_i$ budou $b$-bitová čísla. V praxi přitom bývá počet podílníků mnohem menší než $p$. Říkáme pak, že každému z podílníků musíme zaslat zhruba $b$-bitů informace představující $y_i$, neboť počet bitů nutných k zaznamenání $i$ ve dvojici $(i,y_i)$ lze zanedbat. Shamirovo schéma je zjevně úspornější než Blakleyho, kde každý podílník musel obdržet $(k+1)b$ bitů.
Příklad 2
Mějme nyní čtyři podílníky, kteří chtějí sdílet tajemství $N=6$ tak, že ho mohou zrekonstruovat pouze tehdy, když se sejdou alespoň tři z nich. Rozhodli se zvolit $p=17$. V Blakleyho schématu, kde tajemství představuje první složka řešení soustavy lineárních rovnic, by musel každý uchovávat jednu z rovnic zvolených např. jako \begin{align*} x+2y+3z & = 3,\\ 3x+5y + 4z & = 4,\\ 2x+4y+7z & = 3,\\ 2x+5y+8z & = 3. \end{align*} Jejich jediným řešením v $\mathbb{Z}_{17}^3$ je trojice $(6, 3, 14)$. Každý by si tedy musel pamatovat čtyři čísla. Místo toho v Shamirově shématu stačí, aby každý znal jeden bod $A_i\in\mathbb{Z}_{17}^2$ ze čtveřice \begin{equation}\label{pr:body} A_1=(1,6), \quad A_2=(2,0), \quad A_3=(3,5), \quad A_4=(4, 4). \end{equation} Každá trojice bodů jednoznačně určuje polynom $p(x)=6 + 3x +14 x^2$, takže $N=6$. Pokud se například první dva podílníci rozhodnou své kolegy zradit a společně zjistit sdílené tajemství, má jejich soustava \[ a_0 + a_1\cdot 1 + a_2 \cdot 1 = 6,\qquad a_0 + a_1 \cdot 2 + a_2 \cdot 2^2 = 0 \] v tělese $\mathbb{Z}_{17}$ celkem $p=17$ řešení \[ a_0= 12+ 2 t,\quad a_1 = 11 + 14 t, \quad a_2 = 0 + t, \quad t\in\{0, \ldots , 16\}. \] Zrádci tedy nejsou nalezení $N = a_0 \in \mathbb{Z}_{17}$ o nic blíže než někdo, kdo žádný podíl nemá.
Proaktivní sdílení informace
V praxi je nutné počítat s případem, kdy je prozrazen jeden nebo více podílů na sdílené informaci. Ať už k úniku došlo sofistikovaným útokem nebo nedbalostí, představuje to vážný bezpečnostní problém, kdy je potřeba kompromitované podíly zneplatnit a ty, které protivník nezískal, aktualizovat. Je také samozřejmě potřeba zabránit dalším únikům. Pokud útočníkovi nepadlo do rukou všech $k$ potřebných podílů, umožňuje Shamirovo schéma tuto situaci řešit aniž by bylo nutné měnit sdílené $N$.
Zvolme náhodně polynom \[ q(x)=b_1 x + \ldots + b_{k-1} x^{k-1}, \quad b_j \in \mathbb{Z}_p,\ j\in\{1,\ldots,k-1\} \] s nulovým konstantním členem $b_0=0$ a spočtěme hodnoty $z_i=q(i), i\in\{1,\ldots,n\}$, které rozešleme jednotlivým podílníkům. Ti nahradí své stávající $y_i$ součtem $(y_i+z_i)$ tak, aby informace obsažená v $y_i$ nebyla dále dostupná. Podílníci teď mají v držení funkční hodnoty polynomu $(p+q)(x)$, který má stejný konstantní člen jako polynom $p(x)$. Dříve uniklá data už protivníkovi nejsou k užitku, neboť nemůže získat další $y_i$ příslušející polynomu $p(x)$. Pravidelnou aktualizací podílů lze výrazně zvýšit bezpečnost systému, neboť útočník by musel v omezeném čase nashromáždit $k$ funkčních hodnot z jedné edice. V Blakleyho schématu taková aktualizace možná není. Všimněme si, že pro aktualizaci není třeba znát sdílené tajemství, neboť v $q(x)$ se $N$ nevyskytuje. Je-li potřeba zvýšit minimální počet podílů nutných k určení sdíleného $N$ z $k$ na $l$, kde $k<l\leq n$, lze za $q(x)$ zvolit polynom stupně $l-1$ a stejně jako dříve aktualizovat stávající podíly. Ani pro tento úkon není potřeba znalost $N$. Pro navýšení počtu podílů $n$ ovšem $N$ znát musíme.
Lagrangeova interpolace
Viděli jsme, že použití Shamirova schématu místo Blakleyho může vést ke značné úspoře paměti, neboť každý z podílníků musí uchovávat místo $(k+1)b$ bitů pouze zhruba $b$ bitů. Výhodou Shamirova schématu je ovšem i vyšší efektivita při generování podílů, poněvadž není potřeba ověřovat podmínky na nenulovost determinantů soustav rovnic. V Blakleyho schématu kde je pro zjištění $N$ potřeba alespoň $k$ ze všech $n$ podílníků by bylo potřeba spočíst ${n}\choose{k}$ determinantů, což může být velmi náročné. Tento výpočet nyní odpadá.
Nabízí se otázka, zda je možné v Shamirově schématu urychlit i výpočet sdíleného tajemství. Pokud máme k dispozici $k$ bodů $A_i=(x_i, y_i)$, najdeme koeficienty $a_0, \ldots , a_{k-1}$ interpolačního polynomu $p(x)$ jako řešení soustavy lineárních rovnic \eqref{soustava_interpolace}. Nás ovšem zajímá pouze $a_0 = N$. V některých případech, především pro nízká $k$, lze proto výhodně využít Lagrangeovu interpolaci [3].
Je-li dáno $k$ bodů $A_i=(x_i, y_i), i\in\{1, \ldots, k\}$, kde $x_i\neq x_j \text{ pro } i\neq j$, budeme hledat Lagrangeův interpolační polynom $L(x)$ jako polynom stupně nejvýše $(k-1)$ ve tvaru \begin{equation}\label{Lagrange_poly} L(x) = y_1 l_1(x)+\ldots + y_k l_k(x), \end{equation} kde $l_i(x), i\in\{1, \ldots, k\}$ jsou polynomy stupně $k-1$ pro které platí \begin{equation}\label{podminky_l_i} l_i(x_j)=\left\{\begin{array}{c c} 1 & \text{pro } i=j,\\ 0 & \text{pro } i\neq j. \end{array} \right. \end{equation} Graf takto zkonstruovaného polynomu $L(x)$ bude procházet všemi body $A_i$. V konkrétním bodě $x_i$ bude totiž nenulový právě jeden z polynomů $l_i(x), i\in\{1, \ldots, k\}$ a bude platit \[ L(x_i)=y_i l_i(x_i)=y_i. \] Abychom splnili podmínky \eqref{podminky_l_i}, zkonstruujeme $l_i(x)$ jako \begin{equation}\label{konstrukce_l_i} l_i(x)=\prod_{\substack{1 \leq m \leq k \\ m \neq i}} \frac{x-x_m}{x_i-x_m}=\frac{x-x_1}{x_i-x_1}\ldots\frac{x-x_{i-1}}{x_i-x_{i-1}}\frac{x-x_{i+1}}{x_i-x_{i+1}}\ldots\frac{x-x_k}{x_i-x_k}. \end{equation} Všimněme si, že se skutečně jedná o polynom stupně $k-1$, neboť čitatel obsahuje součin $k-1$ výrazů $(x-x_m), m\in \{1,\ldots, k\}, m\neq i$, obsahujících proměnnou $x$. Oproti tomu jmenovatel obsahuje pouze součin nenulových konstant. V bodě $x_i$ se jednotlivé zlomky pokrátí, takže platí $l_i(x_i)=1$. V bodě $x_j, j\neq i$, bude jeden z činitelů v čitateli nulový, takže platí $l_i(x_j)=0$ pro $j\neq i$. Požadavky \eqref{podminky_l_i} jsou tedy splněny.
Příklad 3
Ukážeme si popsaný postup opět na příkladu čtyřech bodů \eqref{interpolace_body}, kdy budeme hledat kubický polynom jehož graf všemi body prochází. Podle \eqref{konstrukce_l_i} zkonstruujeme jednotlivé $l_i(x)$ jako \begin{align*} l_1(x)&=\frac{(x-x_2) (x-x_3) (x-x_4)}{(x_1-x_2) (x_1-x_3) (x_1-x_4)}=-\frac{2}{15} x^3+\frac{2}{5}x^2-\frac{11}{30}x+\frac{1}{10},\\ l_2(x)&=\frac{(x-x_1) (x-x_3) (x-x_4)}{(x_2-x_1) (x_2-x_3) (x_2-x_4)}=\frac{4}{3}x^3-2 x^2-\frac{4}{3}x+2,\\ l_3(x)&=\frac{(x-x_1) (x-x_2) (x-x_4)}{(x_3-x_1) (x_3-x_2) (x_3-x_4)}= -2 x^3+2 x^2+\frac{5}{2}x-\frac{3}{2},\\ l_4(x)&=\frac{(x-x_1) (x-x_2) (x-x_3)}{(x_4-x_1) (x_4-x_2) (x_4-x_3)}=\frac{4}{5}x^3-\frac{2}{5}x^2-\frac{4}{5}x+\frac{2}{5}. \end{align*} Grafy těchto polynomů můžeme vidět na obrázku 2.
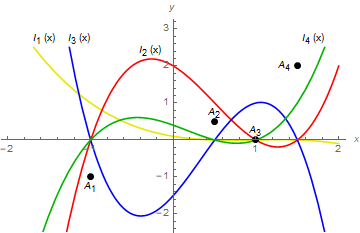
Obrázek 2: Grafy polynomů $l_1(x)$, $l_2(x)$, $l_3(x)$, $l_4(x)$. V každém $x_i$ je nenulový právě jeden polynom $l_i(x)$, který zde nabývá hodnotu $l_i(x_i)=1$.
Výsledný Lagrangeův interpolační polynom \eqref{Lagrange_poly} má tvar \[ L(x)=\frac{12}{5}x^3-\frac{11}{5}x^2-\frac{19}{10}x+\frac{17}{10} \] a jeho graf je spolu s grafy $l_i(x)$ znázorněn na obrázku 3.
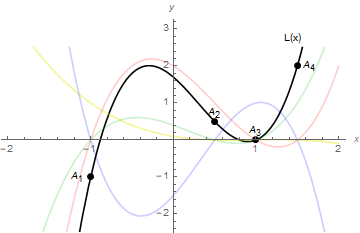
Obrázek 3: Lagrangeův interpolační polynom $L(x)$ procházející body $A_1, A_2, A_3$ a $A_4$.
Jak může Lagrangeova interpolace pomoci při výpočtu sdíleného tajemství $N$? Připomeňme, že $N$ představuje konstantní člen $a_0$ interpolovaného polynomu $p(x)$ a lze jej tedy přímo spočíst jako \[ N = a_0 = L(0) = \sum_{i=1}^k y_i l_i(0)=\sum_{i=1}^k y_i \prod_{\substack{1 \leq m \leq k \\ m \neq i}} \frac{x_m}{x_m-x_i}. \] Tuto formulku můžeme použít i když pracujeme nad konečným tělesem $\mathbb{Z}_p$, jen je třeba mít na paměti, že dělením rozumíme multiplikativní inverzi v modulární aritmetice. V případě $p=17$ a bodů \eqref{pr:body} opět zjistíme, že $N=6$.
V tomto příspěvku jsme se seznámili s Shamirovým schématem, které umožňovalo $n$ podílníkům sdílet pomocí polynomiální interpolace utajenou informaci $N$ tak, že je tuto informaci možno zjistit pouze sejde-li se alespoň $k$ podílníků. Shamirovo schéma jsme porovnali s Blakleyho, abychom ukázali, že je efektivnější nejen díky nižším paměťovým nárokům, ale i díky nižším nárokům výpočetním. Přestože je bezpečnost obou systémů založena na problému hledání řešení soustavy lineárních rovnic, Shamirovo schéma umožňuje pravidelnou aktualizaci podílů a můžeme ho tedy považovat za bezpečnější. Ačkoliv zmiňované systémy nejsou žádnou novinkou, Shamirovo schéma se stále využívá. Téma sdílení tajemství je navíc velmi živé a v oblasti probíhá intenzivní výzkum.
Literatura
- Blakley, G. R., Safeguarding cryptographic keys, American Federation of Information Processing Societies. National Computer Conference, 313-317 (1979)
- Shamir, A., How to share a secret, Communications of the ACM 22, 612-613 (1979).
- Abramowitz, M. and Stegun, I. A. (Eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 878-879 (1972).
Tento článek byl vznikl v rámci řešení projektu Institucionální podpora Českého vysokého učení technického v Praze (CZ.02.2.69/0.0/0.0/16_015/0002382).

